A recent article by Cieslinski, Horsten, and Leitgeb, “Axioms for Typefree Subjective Probability” ends with a proof that the Reflection Principle cannot be consistently added to the axiomatic untyped probability theory which they present.
On the other hand, Haim Gaifman’s “A Theory of Higher Order Probabilities” can be read, despite the glaring difference in interpretation, as establishing the consistency of the Reflection Principle.
Gaifman’s theory is not untyped, and Gaifman’s approach is not axiomatic but model-theoretic. Thus it stays much closer to the original, informal presentation of the Reflection Principle. But it is still noticeably abstract. We can think of his models roughly like this: certain sets of possible worlds are propositions, and there is a function pr which serves to select those propositions that can express factual statements of form “My (or, the agent’s) probability for A equals r”.
What I would like to do here is present a similar theory, staying in closer touch with the original presentation of the Reflection Principle, and entirely explicit about the way the opinion I currently express (about A, say) is constrained to harmonize with my opinions about how that opinion (about A) could change in time to come.
Introduction
The Reflection Principle purports to be an additional criterion of synchronic coherence: it relates current opinion to other current opinions. The principle has both a general form (the General Reflection Principle), but also a form specifically for agents who have opinions about their own (current and/or future) doxastic states. The latter was the original formulation, but should now properly be called the Special Reflection Principle. I will formulate both forms precisely below.
Satisfying Reflection does not require any relation between one’s actual opinions over time. Nevertheless it is pertinent also for diachronic coherence, because it is a constraint on the agent’s current expectation of her future opinions, and because a policy for managing one’s opinion must preserve synchronic coherence.
So a minimal probability model, of an agent whose opinion satisfies Reflection, will consist of a probability function P with a domain that includes this sort of proposition:
(Q) A & my opinion at (current or future) time t is that the probability of A equals r.
I symbolize the second conjunct as pt(A) = r. Hence, symbolically,
(Q) A & pt(A) = r.
Statement pt(A) = r is a statement of fact, true or false, about the agent’s doxastic state at time t. The agent can express opinions about this, as about any other facts.
In contrast I will use capital P to stand for the probability function that encodes the agent’s opinion. This is the opinion that she expresses or would express with statements like “It seems twice as likely as not (to me) that it will snow tonight”. So the sentence P(A) = r is one the agent uses to express such an opinion, and she does this in first-person language.
The (special) Reflection Principle implies a constraint on the opinion expressed in form P(A & pt(A) = r), which relates the opinion expressed about A to the factual statement that the agent has that opinion.
There is in the corresponding language no nesting: nothing of form P( … P …). Whenever the agent expresses an opinion, it is an opinion about matters of fact.
We can proceed in two stages. The first is just to see what the more modest General Reflection Principle is, and how it is to be satisfied. Then we can build on that to do the same for the Special Reflection Principle. I will focus on modeling, and — except at one point — just take it that the relation to a corresponding language will be sufficiently clear.
Stage 1: General Reflection
My current probability for A must lie within the range spanned by the probabilities for A that I may have or come to have at any time t (present or future), as far as my present opinion is concerned.
To illustrate: I am a weather forecaster and realize that, depending on whether a certain storm front moves in during the night, my forecast tomorrow morning will be either 0.2 or 0.8 chance of rain. Then my present forecast for rain must be a chance x of rain tomorrow with x a number in the open interval (0.2, 0.8).
A basic model to represent an agent who satisfies the General Reflection Principle will be the quadruple M = < S, F, TPROB, Pin>, with its elements specified as follows.
T, the set of times, is a linearly ordered finite or countable set with first member (the times). For each t in T, TPROB(t) is a finite set of probability functions. These are functions defined on a field F of sets in space S, with F having S itself as a member. The members of F represent propositions about which, at any time t, I have an opinion, and the members of TPROB(t) are the opinions I could have at time t.
S = <S, F> I will call the basic space. I will use A, B, … for members of F, which I will also call the elementary propositions. The set of probability functions defined on the space S = <S, F> I will call Sp.
At the initial time the agent expresses an opinion, which for now I designate as Pin, consisting in probabilities both for the events represented in space S and about how likely she is to have at time t the various opinions represented in TPROB(t).
The General Reflection Principle requires that for all A in F, Pin(A) is within the span (convex closure, convex hull) of the set {p(A): p is in TPROB(t)}. I will designate that convex closure as [TPROB(t)]. The members of TPROB(t) are the vertices of [TPROB(t)].
Since Pin assigns probabilities to the members of TPROB(t) which are defined on the domain of Pin itself. General Reflection then implies that Pin is a mixture (convex combination) of those members, with the weights thus assigned:
Pin(A) = ∑ {Pin(p)p(A): p in TPROB(t)}
Equivalently, <S, F, Pin > is a probability space, and as it happens, for each t in T, there are appropriate weights such that Pin is a convex combination of the members of TPROB(t).
Pin cannot be more than one thing, so those convex combinations must produce, for each time t, the same initial opinion. We can ensure that this is possible by requiring that for all t and t’, [TPROB(t’)] = [TPROB(t)]. Of course these sets TPROB(t) can be quite different for different times t; the vertices are different, my opinions are allowed to change. And specifically, I will later on have some new certainties, for example after seeing the result of an experiment. What this constraint on the span of foreseen possibilities about my opinion implies for certainties is this:
if today I am not certain whether A, then, if I foresee a possibility that I will become certain that A at a later time, then I foresee also a possibility that I will become certain of the opposite at that time.
SUMMARY: In this construction so far we have Pin defined on a large family of distinct sets, namely the field F of elementary propositions, and each of the sets TPROB(t), for t in T.
The construction guarantees that Pin, in basic model M = <S, F, TPROB, Pin> satisfies the General Reflection principle.
But we have not arrived yet at anything like (Q), and we have not yet given any sense to ‘pt(A) = r’. This we must do before we can arrive at a form in which the Special Reflection Principle is properly modeled.
Stage 2: Special Reflection
The function Pin cannot do all that we want from it, for we need to represent opinions that relate the agent’s probabilities for events in space S to the probabilities assigned to those events by opinions that the agent may have at various (other) times.
Intuitively, (pt(A) = r) is the case exactly if the ‘actual’ opinion at time t is represented by a function p in TPROB(t) such that p(A) = r. In general there may either no, or one, or many members of TPROB(t) which assign probability r to A.
So the proposition in question is thus:
(pt(A) = r) = {p in TPROB(t): p(A) = r}
Since Pin is defined for each p in TPROB(t), Pin assigns a probability to this proposition:
Pin(pt(A) = r) = ∑{Pin(p): p(A) = r and p is in TPROB(t)}.
But what is not well-defined at this point is a probability for the conjunction (*), mentioned above, since A is a member of field F and (pt(A) = r) is a member of a quite different field, of subsets of TPROB(t).
We must depart from the minimalist construction in the preceding section, and extend the function Pin to construct a function P which is well-defined, for each time t, on a larger space. This process is what Dick Jeffrey called Superconditioning.
I have explained its relevant form in the preceding post, with an illustration and intuitive commentary. So I will here proceed a bit more formally than in the preceding post and without much intuitive explanation.
NOTE. At this point we should be a bit more explicit about how the model relates to a corresponding language. Suppose L is a language of sentential logic, and is interpreted in the obvious way in model M: the semantic value [[Q]] of a sentence Q in L is an elementary proposition, that is, a subset of S, a member of field F.
As we now build a larger model, call it M*, by Superconditioning, I need to have a notion of something in M* being ‘the same proposition’ as a given elementary proposition in M. I will use the * notation to do that: there will be relation * between M and M* such that a sentence Q which has value [[Q]] in M has semantic value [[Q]]* in M*.
Quick overview of the final model, restricted to a specific time t:
Given: the basic model defined above, to which we refer in the description of final model M*.
M*(t) = <S*, F*, TPROB*(t), P>, with
S* = S x TPROB(t)
If A is in F then A* = {<x, p>: x is in A, p is in TPROB(t)},
equivalently, A* = A x TPROB(t)
F* is a field of subsets of S* which includes {A*: A is in F}
TPROB*(t) and P, defined on F*, are such that for all A in F, P(A*) = Pin(A)
Construction of the final model, for specific time t
We focus on a specific time t, but the procedure is the same for each t in T. Let TROB(t) = {p1, …, pn}. Each of these probability functions is defined on the space S.
But now we will think instead about the combination of each of these probability functions with S as a separate entity.
For each j, from 1 to n, there is a set Sj = {<x, pj>}: x in S}. Equivalently, Sj = S x {pj}
We define:
for A in F, Aj = {<x, pj>: x is in A},
the field Fj = {Aj : A is in F}.
Clearly Sj = <Sj, Fj> is an isomorphic copy of S, disjoint from Sk unless j = k..
S* = <S*, F*> is the sample space with S* = ∪{Sj : j = 1, …, n}.
Equivalently, S* = S x TPROB(t)
F* is the least field of subsets of S* that includes S* and includes ∪{Fj: j = 1, …, n}.
The sets Sj therefore belong to F* and are the cells in a partition of S*. (These cells represent the distinct situations associated with the different probability functions pj, j = 1, …, n.)
Equivalently, F* is the closure of ∪{Fj: j = 1, …, n} under finite union. This is automatically closed under finite intersection, since each field Fj is closed under intersection, and these fields are disjoint. F* has S* as a member, because S* is the union of all the cells. And the infimumof F* is Λ because that is a member of each cell; note also that Λx TPROB(t) is just Λ.
Clearly, all members of F* are unions of subsets of those cells, specifically finite unions of sets Ak such that A is in F, for certain numbers k between 1 and n, inclusive.
For A in F, we define A* = ∪{Aj : j = 1, …, n}. Clearly, A* = {<x, p>: x in A, p in TPROB(t)}
The function f: A –> A* is a set isomorphism between F and F*. For example,
A* ∩ B* = [∪{Aj : j = 1, …, n}] ∩ [ ∪{Bj : j = 1, …, n}]
= ∪ { Aj ∩ Bj : j = 1, …, n}]
= (A ∩ B)*
Now we come to the probabilities.
Definition. pj* is a probability function on Sj defined by pj*(Aj) = pj(A) for each proposition A in S.
TPROB* = { pj*| j = 1, …, n}
Looking back once again to our basic model we recall that there are positive numbers bj for j = 1, …, n, summing to 1 such that Pin = ∑{bjpj: j = 1, …, n}.
We use these same numbers to define a probability function P on sample space S* as follows:
For j = 1, …,n
- P(Sj) = bj
- for each A in F, P(Aj|Sj) = pj*(Aj).
- Equivalently, for each A in F, P(A* ∩ Sj) = P(Aj) = P(Sj)pj*(Aj).
- P is additive: if A and B are disjoint members of F* then P(A ∪ B) = P(A) + P(B)
Since all members of F* are finite unions of members of the cells Sj, j = 1, …, n it follows that P is defined by this on all members of F*
It is clear that 3. does not conflict with 2. since pj* is additive. Since the weights bj are positive and sum to 1, and each function pj* is a probability function which assigns 1 to Sj it follows that P is a probability function with domain F*, and is the appropriate convex combination of the functions pj*.
P(A*) = ∑ {P(A* ∩ Sj): j = 1, …, n}
= ∑{P(Aj): j = 1, .., n}
= ∑bjpj*(Aj)
= ∑bjpj(A)
= Pin(A)
About the Special Reflection Principle
Define:
(pt(A) = r) = ∪{Sj : P(A*|Sj) = r}
Equivalently,
(pt(A) = r) = ∪{Sj : pj*(Aj) = r}
Since TPROB*(t) is finite, we can switch to a list:
(pt(A) = r) = ∪{Sj : j = k, .., m}
P(pt(A) = r) = ∑ P{Sj : j = k, .., m} = ∑ {bj: j = k, …,m}
With this in hand we now calculate the probability of the conjunction (Q)
A* ∩ (pt(A) = r) = A* ∩ ∪{Sj : j = k, .., m}
= ∪{A ∩ Sj : j = k, .., m}
= ∪{Aj : j = k, .., m}
P(A* ∩ pt(A) = r) = ∑{ P(Aj ): j = k, .., m}
= ∑ {P(Sj)pj*(Aj): j = k, .., m}
= ∑{bjpj*( Aj): j = k, .., m}
= r∑{bj: j = k, .., m}
because for each j = k, …, m, pj*( Aj) = r.
Given both these results, and the definition of conditional probability, we arrive at:
P(A* | pt(A) = r) = r, if defined, that is, if P(pt(A) = r) > 0.
the Special Reflection Principle.
NOTES
1] The same formalism can have many uses and interpretations — just like, in physics, the same equation can represent many different processes. Of course, here “the equation” refers just to the mathematical form, with no reference to meaning or interpretation.
In that sense the Reflection Principle appeared first (as far as I can remember) as Miller’s Principle, connecting subjective probability with objective chance, and used in that sense by David Lewis in his theory thereof.
Then Haim Gaifman, who uses the notation P and pr, gave Miller’s Principle the interpretation that the person expressing her opinion P takes pr to be the opinion of someone(s) or something(s) recognized as expert(s), to which she defers. I have drawn on Gaifman’s theory with that interpretation elsewhere, to give a sense to acceptance of a scientific theory.
2] But the possibility of this sort of reading, which I had mentioned in “Belief and the Will” only to dismiss it for the issue at hand, did promote a misreading of the Reflection Principle. (As David Christensen did, for example.) It would clearly be irrational for me to defer to my future opinion except while supposing that I will then be both of sound mind and more knowledgeable than I am now. But it is not irrational even now to expect myself to be both of sound mind and more knowledgeable, as a result of the sort of good management of my opinion over time, on the basis that I am committed to do so. And this, all the while knowing that I may either be interrupted in this management by events beyond my control or by interrupting myself, in the course of gaining new insights.
This is exactly of a piece with the fact that I can morally promise, for example, to protect someone, and expect myself to keep my promise, and morally expect others to rely on my promise, while knowing — as we all do — the general and irremediable fact that, due to circumstances presently unpredictable, I may fail to do so, either because of force majeure or because of overriding moral concerns. In epistemology must strive for the same subtlety as in ethics.
3] See previous post, “Conditionalizing on a combination of probabilities” for Jeffrey’s concept of Superconditioning and its relation to the informal Reflection Principle.
REFERENCES
Cieslinski, Cezary, Leon Horsten, and Hannes Leitgeb (2022) “Axioms for Typefree Subjective Probability”. arXiv:2203.04879v1
Gaifman, Haim (1988) “A Theory of Higher Probabilities”. Pages 191-219 in Brian Skyrms and William L. Harper (eds.) Causation, Chance and Credence. Dordrecht: Kluwer, 1988.
Van Fraassen, Bas C. (1995) “Belief and the Problem of Ulysses and the Sirens.” Philosophical Studies 77: 7–37.



 Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true:
Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true: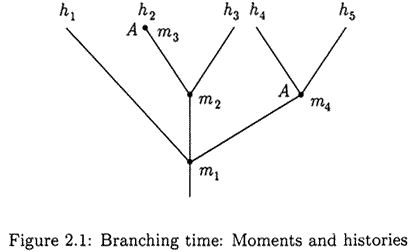 If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.
If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.