Seminal text: Nicholas Rescher, The Logic of Commands. London: 1966
- Imperatives: the three-fold pattern 1
- Denoting imperatives 2
- Identifying imperatives through their truthmakers 2
- Entailment and logical combinations of imperatives 3
- Starting truthmaker semantics: the events. 4
- Event structures 4
- The language, imperatives, and truthmakers 5
- Logic of imperatives 6
APPENDIX. Definitions and proofs 7
In deontic logic there was a sea change when imperatives were construed as default rules (Horty, Reasons as Defaults: 2012). The agent is conceived as situated in a factual situation but subject to a number of ‘imperatives’ or ‘commands’.
Imperatives can be expressed in many ways. Exclamation marks, as in “Don’t eat with your fingers!”, may do, but are not required. Adapting one of Horty’s examples, we find in a book of etiquette:
- One does not eat food with one’s fingers
- Asparagus is eaten with one’s fingers
These are declarative sentences. But in this context they encode defeasible commands, default rules. Reading the book of etiquette, the context in question, we understand the conditions in which the indicated actions are mandated, and the relevant alternatives that would constitute non-compliance.
In this form of deontic logic, what ought to be the case in a situation is then based on the facts there plus the satisfiable combinations of commands in force.[1]
1. Imperatives: the three-fold pattern
Imperatives have a three-fold pattern for achievement or lack thereof:
- Success: required action carried out properly
- Failure: required action not carried out properly or not at all
- Moot: condition for required action is absent
In the first example above, the case will be ‘moot’ if there is no food, or if you are not eating. Success occurs if there is food and it is not eaten with the fingers, Failure if there is food and it is eaten with the fingers.
Whenever this pattern applies, we can think of that task as having to be carried out in response to the corresponding imperative. There are many examples that can be placed in this form. For example, suppose you buy a conditional bet on Spectacular Bid to win in the Kentucky Derby. Doing so imposes an imperative on the bookie. He is obligated to pay off if Spectacular Bid wins, allowed to keep the money if she loses, and must give the money back if she does not run.
2. Denoting imperatives
An imperative may be identified in the form ‘When A is the case, see to it properly that B’. This way of identifying the imperative specifies just two elements of the three-fold pattern, Success and (the opposite of) Moot.
But the opposite of Moot is just the disjunction of the two contraries in which the condition is present. Therefore it is equally apt to represent the imperative by a couple of two contraries, marking Success and Failure. Doing so gives us a better perspective on the structure of imperatives and their relation to ‘ought’ statements.
So I propose to identify an imperative with an ordered pair of propositions <X, Y>, in which X and Y are contraries. Intuitively they correspond respectively to Success (and not Moot), and Failure (and not Moot).
3. Identifying imperatives through their truthmakers
Our examples point quite clearly to a view of imperatives that goes beyond truth conditions of the identifying propositions. What makes for success or failure, what makes for the truth of the statement that the imperative has been met or not met, are specific events.
That Spectacular Bid wins, or that you close the door when I asked you to, are specific facts or events which spell success. That I eat the asparagus with a fork is a distinct event which spells a failure of table etiquette.
Consider the command
(*) If A see to it that B!
as identified by its two contraries, Success and Failure. For each there is a class of (possible) events which ‘terminate’ the command, one way or the other.
The statement “Spectacular Bid wins” states that a certain event occurs, and encodes a success for the bookie’s client. The statement that encodes Failure is not “Spectacular Bid does not win”. Rather it is “Spectacular Bid runs and does not win”, which is, for this particular imperative the relevant contrary.
To symbolize this identification of imperatives let us denote as <X| the sets of events that make X true, and as |X> the set of events that make the relevant contrary (Failure) true.[2] The imperative in question is then identified by an ordered couple of two sets of events, namely (<X|, |X>). I will abbreviate that to <X>.
In (*), <X> is the imperative to do B if A is the case, so X = the statement that (A and it is seen to that B), which is made true by all and only the events in set <X|. Its relevant contrary in this particular imperative is the statement that (A but it is not seen to that B), and that relevant contrary is whatever it is that is made true by all and only the events in set |X>.
4. Entailment and logical combinations of imperatives
There is an obvious sense in which E, “Close the door and open the window!” entails F, “Close the door!” Success for E entails success for F. But that is not all. Failure for F entails failure for E. The latter does not follow automatically from the former, if there is a substantial Moot condition: not winning the Derby does not, as such, imply losing.
So entailment between imperatives involves two ‘logical’ implications, going in opposite directions, and we can define:
Definition. Imperative A entails imperative B exactly if <A| ⊆ <B| and |B> ⊆ |A>.
“Open the door!” is a ‘strong’ contrary to “Close the door!”. There is a weaker contrary imperative: if someone looks like he is about to close the door, you may command “Do not close the door!”.
Negation. In the logic of statements, the contradictory is precisely the logically weakest contrary. For example, yellow is contrary to red and so is blue, but to be simply not red is to be either yellow or blue or … and so forth.
So I propose as the analogue to negation that we introduce
<┐A>: <┐A| = |A> and |┐A> = <A|
Whatever makes ┐A true is what makes A false, and vice versa. Here the symbol “┐” does not stand for the usual negation of a statements, because imperatives generally have significant, substantial conditions. The relevant contrary to Success is not its logical contradictory (that would be: either Failure or Moot) but Failure (which implies not-Moot), and that is whatever counts as Failure for the particular imperative in question.
Conjunction. “Close the door and open the window” we can surely symbolize as <A & B>. Success means success for both. In addition, failure means failure for one or the other or both. So there is no great distance between conjunction of Success statements and the ‘meet’ operation on imperatives:
<A & B>: <A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>.
Disjunction. Similarly, dually, for disjunction and the ‘join’ operation:
<A v B>: <A v B| = <A| ∪ <B|, |A v B> = |A> ∩ |B>
We can already see that some familiar logical relations are making an appearance.
[1] <A & B> entails <A>, while <A> entails <A v B>.
For example, <A & B| ⊆ <A| and |A> ⊆ |A & B>.
(All proofs will be provided in the Appendix.)
We could go a bit further with this. But answers to the really interesting questions will depend on the underlying structure of events or facts, that is, of the truthmakers.
5. Starting truthmaker semantics: the events.
Events combine into larger events, with an analogy to conjunction of statements. So the events form a ‘meet’ semilattice. Important are the simple events:
Postulate: Each event is a unique finite combination of simple events.
Is it reasonable to postulate this unique decomposability into simple events?
At least, it is not egregious. Think of how we specify a sample space for probability functions: each measurable event is a subset of the space. The points of the space may have weights that sum up to the measure of the event of which they are the members. Two events are identical exactly if they have the same members.
In any case, the idea of truthmakers is precisely to have extra structure not available in possible worlds semantics.
Combination we can conceive of as a ‘meet’ operation. Besides combining, we need an operation to identify contraries among events, in order to specify Success and Failure of imperatives.
Definition. A event structure is a quadruple E = <E, E0, ., ° >, where E is a non-empty set, . is a binary operation on E, E0 is a non-empty subset of E, and ° is a unary operation on E0, such that:
- ° is an involution: if a is in E0 then a° ≠ a and a°° = a
- . is associative, commutative, idempotent (a ‘meet’ operator)
- If e and e’ are elements of E then there are elements a1, …, ak, b1, …, bm of E0 such that e = a1… ak, and e’=b1…bm and e = e’ if and only if { a1, …, ak }= { b1, …, bm }
This last clause implies along the way that if e is an element of E then there is a set a1, …, an of elements of E0 such that e = a1 … an. That is part, but only part, of what the Postulate demands, and would not by itself imply unique decomposability.
The involution operates solely on simple events. A particular imperative could have a simple event b to identify Success; in that case simple event b° will be identify its Failure.
6. Event structures
The following definitions and remarks refer to such an event structure E.
Definition. e ≤ e’ if and only if there is an event f such that e’.f = e.
Analogy: a conjunction implies its conjuncts, and if A implies B then A is logically equivalent to (A & C) for some sentence C.
The definition is not the standard one, so we need to verify that it does give us a partial order, fitting with the meet operator.
[2] The relation ≤ is a partial ordering, and e.f is the glb of e and f.
That is, we have the familiar semilattice laws: e.g. if e ≤ e’ and f is any other event then f.e ≤ e’.
So <E, ., ≤ > is a meet semilattice. Note also that if a and b are simple events then a ≤ b only if a = b. For if b.f = a, the Postulate implies that b = f = a.
So far we have a relation of contrariety for simple events only. For events in general we need to define a general contrariness relationship.
Definition. Event e is contrary to event e’ if and only if there is an event a in E0 such that e ≤ a and e’ ≤ a° .
Contrariety is symmetric because a°° = a.
At this point we can see that the logic we are after will not be classical. For contrariety is not irreflexive.
That is because (a.a°) ≤ a and (a.a°) ≤ a°, so (a.a°) is contrary to itself. But (a.a°) is not the bottom of the semilattice. If a, a°, and b are distinct simple events then it is not the case that (a.a°) ≤ b. For if b.f = a.a° and f = a1 … an then the Postulate requires {b, a1, …, an} = {a, a°} so either b = a or b = a° .
It is tempting to get rid of this non-classical feature. Just reducing modulo some equivalence may erase the distinction between those impossible events, a.a° and b.b° . Such events can never occur anyway.
But there are two reasons not to do so. The first is that the history of deontic logic has run on puzzles and paradoxes that involve apparent self-contradictions. The second is more general. We don’t know what new puzzles may appear, whether about imperatives or related topics, but we hope to have resources to represent whatever puzzling situation we encounter. Erasing distinctions reduces our resources, and why should we do that?
7. The language, imperatives, and truthmakers
More formally now, let us introduce a language, and call it LIMP. Its syntax is just the usual sentential logic syntax (atomic sentences, &, v, ┐). The atomic sentences will in a specific application include sentences in natural language, such as ‘”One does not eat with one’s fingers”. The interpretations will treat those sentences not as statements of fact but as encoding imperatives. In each case, the interpretation will supply what a context (such as a book of etiquette) supplies to set up the coding.
An interpretation of language LIMP in event structure E = <E, E0, ., ° > begins with a function f that assigns a specific event to each atomic sentence in each situation. Then there are two functions, < | and | >, which assign sets of truth-makers to each sentence:
- If A is atomic and a = f(A) then <A| = {e in E: e ≤ a} and |A> = {e in E: e ≤ a°}.
- <┐A| = |A> and |┐A> = <A|
- <A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>
- <A v B| = <A| ∪ <B|, |A v B> = |A> ∩ |B>
Definition. A set X of events is downward closed iff for all e, e’ in E, if e ≤ e’ and e’ is in X then e is in X.
[3] For all sentences A, <A| and |A> are downward closed sets.
Now we can also show that our connector ┐, introduced to identify the weakest contrary to a given imperative, corresponds (as it should) to a definable operation on sets of events.
Definition. If X ⊆ E then X⊥ = {e: e is contrary to all elements of X}.
I will call X⊥ the contrast (or contrast class) of X.
Lemma. X⊥ is downward closed.
That is so even if X itself is not downward closed. For suppose that f is in X⊥. Then for all members e of X there is a simple event a such that f ≤ a and e ≤ a°. Thus for any event g, also g.f.e ≤ a while e ≤ a°. Therefore g.f is also in X⊥.
[4] For all sentences A, <┐A| = |A> = <A|⊥ and |┐A> = <A| = |A> ⊥ .
The proof depends De Morgan’s laws for downward closed sets of events:
Lemma. If X and Y are downward closed sets of events then
(X ∩ Y) ⊥ = X ⊥ ∪ Y ⊥ and (X ∪ Y) ⊥ = X ⊥ ∩ Y ⊥.
In view of [4], there is therefore an operator on closed sets of events that corresponds to negation of imperatives:
Definition. If A is any sentence then <A> ⊥ = (<A| ⊥ , |A> ⊥ ).
[5] <A> ⊥ = <┐A>
This follows at once from [4] by this definition of the ⊥ operator on imperatives.
8. Logic of imperatives
We will concentrate here, not on the connections between sentences A, but on connections between their semantic values <A>. These are the imperatives, imperative propositions if you like, and they form an algebra.
Recall the definition of entailment for imperatives. It will be convenient to have a symbol for this relationship:
Definition. <A> ⇒ <B> exactly if <A| ⊆ <B| and |B> ⊆ |A>.
The following theorems introduce the logical principles that govern reasoning with imperatives.
[6] Entailment is transitive.
To have the remaining results in reader-friendly fashion, let’s just summarize them.
[7] – [11]
- Meet.
- <A & B> ⇒ <A>,
- <A & B> ⇒ <B>
- If <X> ⇒ <A> and <X> ⇒ <B> then <X> ⇒ <A & B>
- Join.
- <A> ⇒ <A v B>
- <B> ⇒ <A v B>
- If <A> ⇒ <X> and <B> ⇒ <X> then <A v B> ⇒ <X>
- Distribution: <A &(B v C)> ⇒ <(A & B) v (A & C)>.
- Double Negation. <A> ⇒ < ┐ ┐ A> and < ┐ ┐ A> ⇒ <A>.
- Involution. If <A> ⇒ <B> then <┐B> ⇒ <┐A>.
- De Morgan.
- < ┐ (A & B)> ⇒ < ┐A v ┐B> and vice versa
- < ┐ (A v B)> ⇒ < ┐A & ┐B> and vice versa.
COMMENTS. In order for these results to make proper sense, each of the connectors ┐, &, v needs to correspond to an operator on imperatives, modeled as couples of downward closed sets of events. This was shown in the previous section.
The logic of imperatives is not quite classical. We can sum up the above as follows:
The logic of imperatives mirrors FDE (logic of first degree entailment); the imperatives form a De Morgan algebra, that is, a distributive lattice with De Morgan negation.
APPENDIX. Definitions and proofs
Definition. Imperative A entails imperative B exactly if <A| ⊆ <B| and |B> ⊆ |A>.
[1] <A & B> entails <A>, and <A> entails <A v B>.
For <A & B| = <A| ∩ <B| ⊆ <A| while |A > ⊆ |A|> ∪ |B> = |A & B>. Similarly for the dual.
Postulate: each event is a unique finite combination of simple events.
Definition. A event structure is a quadruple E = <E, E0, ., ° >, where E is a non-empty set, . is a binary operation on E, E0 is a non-empty subset of E, and ° is a unary operation on E0, such that:
- ° is an involution: a° ≠ a and a°° = a, if a is in E0
- . is associative, commutative, idempotent (a ‘meet’ operation)
- If e and e’ are elements of E then there are elements a1, …, ak, b1, …, bm of E0 such that e = a1… ak, and e’=b1…bm and e = e’ if and only if { a1, …, ak }= { b1, …, bm }
[2] The relation ≤ is a partial ordering, and the meet e.f of e and f is the glb of e and f.
For e ≤ e because e.e = e (reflexive), and if e = e’.f and e’ = e”.g then e = e”.f.g (transitive).
(Perhaps clearer: For if e = e’.f then e.g = e’.f.g, so if e ≤ e’ then e.g ≤ e’, for all events g.)
Concerning the glb:
First, e.f ≤ e because there is an element g such that e.f .g = e. g, namely g = f.
Secondly suppose e’ ≤ e, and e’ ≤ f. Then there are g and h such that e.g = e’ and f.h = e’. In that case e’ = g.h.f.e, and therefore e’ ≤ e.f.
Definition. Event e is contrary to event e’ if and only if there is an event a in E0 such that e ≤ a and e’ ≤ a° .
Contrariness is symmetric because a°° = a. But it is not irreflexive for (a.a°) ≤ a and (a.a°) ≤ a°.
Lemma 1. If a and b are simple events then a ≤ b only if a = b.
That is because decomposition into simple events is unique. For suppose that a.f = b. Then there are simple events c1, …, ck such that f = c1….ck and a.f = a. c1, …, ck = b, which implies that a = c1 = … = ck = b.
Interpretation of the imperatives expressed in language LIMP, in event structure E = = <E, E0, ., ° >, relative to function f from atomic sentences to simple events. Then there are two functions, < | and | >, which assign sets of truth-makers to each sentence:
- If A is atomic and a = f(A) then <A| = {e in E: e ≤ a} and |A> = {e in E: e ≤ a° }.
- <┐A| = |A> and |┐A> = <A|
- <A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>
- <A v B| = <A| ∪ <B|, |A v B> = |A> ∩ |B>
Definition. A set X of events is downward closed iff for all e, e’ in E, if e ≤ e’ and e’ is in X then e is in X.
[3] For all sentences A, <A| and |A> are downward closed sets.
Hypothesis of induction: this is so for all sentences of length less than A.
Cases.
- A is atomic. This follows from the first of the truth-maker clauses
- A has form ┐B. Then <B| and |B> are downward closed, and these are respectively |┐A> and <┐A|.
A has the form (B & C) or (B & C). Here it follows from the fact that intersections and unions of downward closed sets are downward closed.
Definition. If X ⊆ E then X⊥ = {e: e is contrary to all elements of X}
Lemma 2. X⊥ is downward closed.
Suppose that e is in X⊥. Then for all e’ in X, there is a simple event a such that e ≤ a and e’ ≤ a . This implies for any event f, that f.e ≤ a and e’ ≤ a . Hence f.e is also in X⊥.
[4] For all sentences A, <┐A| = |A> = <A|⊥ and |┐A> = <A| = |A> ⊥ .
Hypothesis of induction: If B is a sentence of length less than A then <┐B| = |B> = <B|⊥ and |┐B> = <B| = |B> ⊥ .
Cases.
- A is atomic, and f(A) = a. Then by the first truth-maker clause, all elements of |A> are contrary to all of <A|. Suppose next that e is contrary to all of <A|, so e is contrary to a, hence there is a simple event b such that a ≤ b and e ≤ b° . But then a = b, so e ≤ a° , hence e is in |A>. Similarly all elements of <A| are contrary to all elements of |A>, and the remaining argument is similar.
- A has form ┐B. Then by hypothesis <┐B| = |B> = <B|⊥ . And <┐┐B| = |┐B> by the truthmaker conditions, and |┐B> = <B|, and the hypothesis applies similarly to this.
- A has form (B & C)
We prove first that <┐A| = |A> = <A| ⊥
<A| = <B| ∩ <C|, while <┐A| = |B & C> = |B> ∪ |C>. If e is in <┐A| then it is in |B> ∪ |C> so by hypothesis e is contrary either to all of <B| or to all of <C|, and hence to their intersection.
Suppose next that e is in <A|⊥ = (<B| ∩ <C|)⊥ . To prove that this is <┐A| = <┐(B & C)| = |B & C> = |B> ∪ |C> = <B|⊥ ∪ <C|⊥ it is required, and suffices, to prove the analogues to De Morgan’s Laws for downward closed sets. See Lemma below.
We prove secondly that |┐A> = <A| = |A> ⊥ . The argument is similar, with appeal to the same Lemma below.
(4) A has form (B v C). The argument is similar to case (3), with appeal to the same Lemma below.
Lemma 3. De Morgan’s Laws for event structures: If X and Y are downward closed sets of events then (X ∩ Y) ⊥ = X ⊥ ∪ Y ⊥ and (X ∪ Y) ⊥ = X ⊥ ∩ Y ⊥.
Suppose e is in X ⊥. Then e is contrary to all of X, hence to all of X ∩ Y, hence is in (X ∩ Y) ⊥. Similarly for e in Y ⊥. Therefore (X ⊥ ∪ Y ⊥ ) ⊆ (X ∩ Y) ⊥.
Suppose on the other hand that e is in (X ∩ Y) ⊥. Suppose additionally that e is not in X⊥. We need to prove that e is in Y ⊥.
Let e’ be in X and not contrary to e. Then if e’’ is any member of Y, it follows that e’.e’’ is in X ∩ Y, since X and Y are both downward closed. Therefore e is contrary to e’.e’’. We need to prove that e is contrary to e”.
Let b be a simple event such that e ≤ b and e’.e” ≤ b°. By our postulate, e’ and e’’ have a unique decomposition into finite meets of simple events. So let e’ = a1…ak and e’’= c1…cm, so that e’.e” = a1…ak.c1…cm. Since e’.e” ≤ b°, there is an event g such that a1…ak.c1…cm = e’.e’’= g.b°. The decomposition is unique, so b° is one of the simple events a1, …, ak, c1, …, cm. Since e is not contrary to e’, it follows that none of a1, …, ak is b°. Therefore, for some j in {1, ..,m}, cj = b°, and therefore there is an event h such that e” = h. b°, in other words, e” ≤ b°. Therefore e is contrary to e”.
So if e is not in X ⊥ then it is in Y ⊥, and hence in X ⊥ ∪ Y ⊥.
The argument for the dual equation is similar.
In view of the above, there is an operator on closed sets of events that corresponds to negation of imperatives:
Definition. If A is any sentence then <A> ⊥ = (<A| ⊥ , |A> ⊥ ).
[5] <A> ⊥ = <┐A>
(<A| ⊥ , |A> ⊥ ) = (<┐A|, |┐A>), in view of [4].
Definition. <A> ⇒ <B> exactly if <A| ⊆ <B| and |B> ⊆ |A>.
The following theorems introduce the logical principles that govern reasoning with imperatives.
[6] Entailment of imperatives is transitive.
Suppose <A> ⇒ <B> and <B> ⇒ <C>. Then <A| ⊆ <B| and <B| ⊆ <C|, hence <A| ⊆ <C|. Similarly, |C> ⊆|A>.
[7] <A & B> ⇒ <A>, and if <X> ⇒ <A> and <X> ⇒ <B> then <X> ⇒ <A & B>, Also <A> ⇒ <A v B>, and if <A> ⇒ <X> and <B> ⇒ <X> then <A v B> ⇒ <X>
First, <A| ∩ <B| ⊆ <A| and |A> ⊆ |A> ∪ |B>, hence <A & B> ⇒ <A>.
Secondly, suppose that X is such that <X| ⊆ <A| and <X| ⊆ <B| while |A> ⊆ |X> and |B> ⊆ |X>. Then <X| ⊆<A| ∩ <B| = <A& B| while |A & B> = |A> ∪ |B> ⊆ |X>. Hence <X> ⇒ <A & B>.
The dual result for disjunction by similar argument.
[8] Distribution: <A &(B v C)> ⇒ <(A & B) v (A & C)>.
<A &(B v C)| = <A| ∩ <B v C| = <A| ∩ (<B| ∪ <C|) = [<A| ∩ <B| ] ∪ [<A| ∩ <C|)] = <(A & B) v (A & C|. Similarly for the other part.
[9] Double Negation: <A> ⇒ < ┐ ┐ A> and < ┐ ┐ A> ⇒ <A>.
< ┐ ┐ A| = |┐ A> = <A| and |┐ ┐ A> = <┐ A| = |A>
[10] Involution. If <A> ⇒ <B> then <┐B> ⇒ <┐A>.
<┐B> ⇒ <┐A> exactly if <┐B| ⊆ <┐A|, i.e. |B> ⊆ |A>, and |┐A> ⊆ |┐B>, i.e. <A| ⊆ <B|. But that is exactly the case iff <A> ⇒ <B>
[11] De Morgan. < ┐ (A & B)> ⇒ < ┐A v ┐B> and vice versa, while < ┐ (A v B)> ⇒ < ┐A & ┐B> and vice versa.
< ┐ (A & B)| = |A & B> = |A> ∪ |B> = < ┐A| ∪ < ┐B| = < ┐A v ┐B|. Similarly for |┐(A & B> . Therefore < ┐ (A & B)> = < ┐A v ┐B>.
Similarly for the dual.
7. REFERENCES
Curry, Haskell B. (1963) Foundations of Mathematical Logic. New York: McGraw-Hill.
Lokhorst, Gert-Jan C. (1999) “Ernst Mally’s Deontik”. Notre Dame Journal of Formal Logic 40 : 273-282.
Mally, Ernst (1926) Grundgesetze des Sollens: Elemente der Logik des Willens. Graz: Leuschner und Lubensky
Rescher, Nicholas (1966) The Logic of Commands. London: Routledge and Kegan Paul
NOTES
[1] Rescher traces this analysis of ‘ought’ statements to Ernst Malley (1926) who coined the name Deontik for his ‘logic of willing’. Since the logic of imperatives we arrive at here is non-classical, note that Lokhorst (1999) argues that Mally’s system is best formalized in relevant logic.
[2] We can use Dirac’s names for them, “bra” and “ket”, with no reference to their original use.



 In the diagram K1 is the set of possible histories h1 and h2, and so CA(h1,t) = K1 = CA(h2, t). (Note well: I speak in terms of instants t of time, rather than Horty’s moments.
In the diagram K1 is the set of possible histories h1 and h2, and so CA(h1,t) = K1 = CA(h2, t). (Note well: I speak in terms of instants t of time, rather than Horty’s moments. In the first example the point made is that according to the above analysis, it is generally the case that the agent ought to gamble, since the best possible outcome is to win the gamble, and that is possible only if you gamble. That is implausible on the face of it — and in that first example, we see that the gambler could make sure that gets 5 units by not gambling, which looks like a better option than the gamble, which may end with a gain of 10 or nothing at all. While someone who values gambling for its own risk might agree, we can’t think that this is what he ought to do. The second example is the same except that winning the gamble would only bring 5 units, with a risk of getting 0, while not gambling brings 5 for sure. In this case we think that he definitely ought not to gamble, but on the above analysis it is not true either that he ought to gamble or ought not to gamble.
In the first example the point made is that according to the above analysis, it is generally the case that the agent ought to gamble, since the best possible outcome is to win the gamble, and that is possible only if you gamble. That is implausible on the face of it — and in that first example, we see that the gambler could make sure that gets 5 units by not gambling, which looks like a better option than the gamble, which may end with a gain of 10 or nothing at all. While someone who values gambling for its own risk might agree, we can’t think that this is what he ought to do. The second example is the same except that winning the gamble would only bring 5 units, with a risk of getting 0, while not gambling brings 5 for sure. In this case we think that he definitely ought not to gamble, but on the above analysis it is not true either that he ought to gamble or ought not to gamble. Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true:
Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true: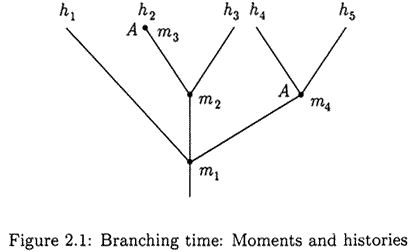 If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.
If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.