evidence – Bas van Fraassen's philosophy blog

In an earlier post, “Subjective probability and a puzzle about theory confirmation” I proposed that we distinguish between confirmation and evidential support. But the words “evidence” and “confirmation” have been so closely linked in the literature, and probably in common use as well, that it may be hard to make such a distinction.

Here I will use an example (more or less historical) to show how it can be natural to distinguish evidential support from confirmation, and why evidential support is so important apart from confirmation. (At the end I’ll take up how that relates to the puzzle set in the earlier blog.)

Cartesian physics did not die with Descartes, and Newton’s theory too had to struggle for survival, for almost a century. In an article in 1961 Thomas Kuhn described the scientific controversy in the 18th century, focused on the problem

“of deriving testable numerical predictions from Newton’s three Laws of motion and from his principle of universal gravitation […]The first direct and unequivocal demonstrations of the Second Law awaited the development of the Atwood machine, … not invented until almost a century after the appearance of the Principia”.

Descartes had admitted only quantities of extension (spatial and temporal) in physics, these being the only directly measurable ones. Newton had introduced the theoretical quantities of mass and force, and the Cartesian complaint was that this brought in unmeasurable ‘occult’ quantities.

The Newtonians’ reply was: No, mass and force are measurable! The Atwood machine was a putative measurement apparatus for the quantity mass.

This ‘machine’ described by the Reverend George Atwood in 1784 is still sometimes used in classroom demonstration experiments for Newtonian mechanics. Atwood describes the machine, pictured below, as follows:

“The Machine consists of two boxes, which can be filled with matter, connected by an string over a pulley. … Result: In the case of certain matter placed in the boxes, the machine is in neutral equilibrium regardless of the position of the boxes; in all other cases, both boxes experience uniform acceleration, with the same magnitude but opposite in direction.”

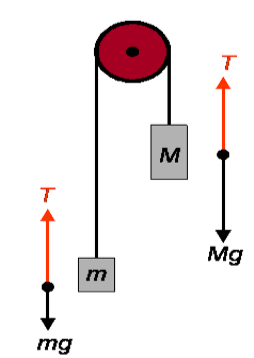
Newton’s second law implies that the acceleration equals g[(M-m)/(M+m)]. Assuming the second law, therefore, it is possible to calculate values for the theoretical quantities from the empirical results about the recorded acceleration. The value of g is determined via the acceleration of a freely falling body (also assuming the second law), hence after measuring the acceleration a short calculation then determines the mass ratio M/m.

How does this strike a Cartesian? Their obvious reply must surely be that Atwood didn’t at all show that Newtonian mass is a measurable quantity! He was begging the question, for he was assuming principles from Newton’s theory.

Not only did Atwood not do anything to show that Newtonian mass is a measurable quantity, except relative to Newtonian physics (= on the assumption that the system is a Newtonian system) — he did not do anything to confirm Newton’s theory, in Cartesian eyes. From their point of view, or from any impartial point of view, this was a petitio principii.

But Cartesians had no right to sneer. For Atwood opened the road to the confirmation of many empirical results, brought to light by Newton’s approach to physics.

First of all it was possible to confirm concordance in all the results from using Atwood’s machine, and secondly their concordance with results of other empirical set-ups that counted as measurements of mass for Newtonian physics. In addition, as Mach pointed out later in his discussion of Atwood’s machine, it made it possible to measure with greater precision the constant acceleration postulated in Galileo’s law of falling bodies, a purely empirical quantity.

It was Atwood’s achievement here to show that the theory was, with respect to mass at least, empirically grounded: mass is measurable under certain conditions relative to (or: supposing) Newton’s theory, and there is concordance in the results of such measurements. When that is so, for quantities involved in the theory, and only when that is so, is the theory applicable in practical, empirically specifiable situations, for prediction and manipulation.

This is what I want to give as paradigm example of evidential support. Newton’s theory was rich enough to allow for the design of Atwood’s machine, with results that are significant and meaningful relative to that theory. Certainly there was a lot of confirmation, namely of empirical regularities and correlations, brought to light and put to good practical use, thereby demonstrating that Newton’s theory was a good, well-working theory in physics. Whether the description of nature in terms of Newton’s theoretical quantities was thereby confirmed in Cartesian or anyone else’s eyes, ceased to matter.

In the earlier blog I showed how a theory’s initial postulate could remain un-confirmed while the theory as a whole is being confirmed, in tests of its empirical consequences. If we just think about the updating of our subjective probabilities then that initial postulate would never become more likely to be true (and of course the entire theory cannot get to be more likely to be true than that initial part!).

But the evidential support for the theory, which is gained by a combination of empirical results and calculations based on the theory itself (in the style of Glymour’s ‘bootstrapping’) extends to all parts of the theory, including the initial postulates. So evidential support, which comes from experiments whose design is guided the theory itself, and whose results are understood in terms of that very theo outstrips confirmation, and should be distinguished from confirmation.

A new scientific (or quasi-scientific) theory often begins with a flamboyant, controversial new postulate. Just think of Copernicus’ theory that starts with the postulate that the Sun is stationary and the earth moving. Or Dalton’s, that all substances are composed of atoms, which combine in molecules in remarkable ways. Or von Daniken’s, that the earth has had extra-terrestrial visitors.

The first reaction is usually that this sort of speculation can’t even be tested. But the theory is developed, with many new additions, and eventually a testable consequence appears. When that is tested, and the result is positive, the theory is said to be confirmed.

I will take it here that “confirm” has a very specific meaning: that information confirms a theory if and only if it makes that theory more likely to be true. And in addition, I will take the “likely” to be a subjective probability: my own, but it could be yours, or the community’s. So, using the symbolism I introduced in the previous post (“Moore’s Paradox and Subjective Probability”) the relation is this:

Information E confirms theory T if and only if P(T | E) > P(T)

Now, the question I want to raise is this:

In this sort of scenario, does the confirmation of the theory also raise the probability that the initial flamboyant postulate is true?

I will argue now that in general, the answer to this question must be NO. The reason is that from the prior point of view, what is eventually tested is not relevant to that initial postulate — though of course it is relevant to that postulate relative to the developed theory.

The answer NO must, I think, be surprising at first blush. But I will blame that precisely on a failure to distinguish prior relevance from relevance relative to the theory.

I will present the argument in two forms — the first quick and easy, the second a bit more finicky (relegated to the Appendix).

For my first argument I will represent the impact of the positive test as a Jeffrey Conditionalization. The testable consequence of the theory is a proposition (or if you prefer the terminology, an event) B, in a probability space S.

The prior probability function I will call P as usual, the posterior probability function P*. Let q = P(B). Then, for any event Y in S,

P(Y) = qP(Y|B) + (1 – q)P(Y| ~B)

Now when the test is performed, the impact on our subjective probability is that the probability of B is raised from q to r. Jeffrey’s recipe for the posterior probability P* is simple: all probability ratios ‘inside’ B or ‘inside’ ~B are to be kept the same as they were. Hence:

for all events Y in S, P*(Y) = rP(Y|B) + (1 – r)P(Y| ~B)

In general there can be quite a large redistribution of probabilities due to such a Jeffrey shift. However, something remains the same. Both the above formulas, for P and for P*, assign to each event Y a number that is a convex combination of two end points, namely P(Y|B) and P(Y| ~B).

What is characteristic of a convex combination is that it will be a number between the two end points.

So in the case in which Y and B are mutually irrelevant, from a prior point of view, those two endpoints are the same:

P(Y|B) = P(Y| ~B) = P(Y)

hence any convex combination of those two is also just precisely that number

Application: Suppose A is the initial flamboyant postulate of the theory. Typically, from the prior point of view, there is no relevance between A and the eventual tested consequence of the entire theory, B. So the prior probability P is such that P(A|B) = P(A |B). Therefore, when the positive evidence comes in (and the probability of the entire theory rises!) the probability of that initial flamboyant postulate stays the same.

For example, in Dalton’s time, 1810, when he introduced the atomic hypothesis into chemistry, the prior probabilities were such that any facts about Brownian motion were irrelevant to that hypothesis. (Everyone involved was ignorant of Lucretius argument about the movement of dust particles, and although the irregular movement of coal dust particles had been described by the Dutch physiologist Jan Ingen Housz in 1785, the phenomenon was not given serious attention until Brown discussed it in 1827.)

So when, after many additions and elaborations of the atomic theory had made it into a theory that had a testable consequence in data about Brownian motion (1905), that full theory was confirmed in everyone’s eyes, but the initial hypothesis about unobservable atomic structure did not become any more likely than it was in 1810.

Right?

And notice this: the entire theory is in effect a conjunction of the initial postulate with much else. But a conjunction is never more likely to be true than any of its conjuncts. So the atomic theory is not now more likely to be true than it was in Dalton’s time.

Confirmation of empirical consequences raises the probability of the theory as a whole, but it is a matter of increase in a very low probability, below that of its initial postulate, which never rises above that.

My Take On This

The confirmation of empirical consequences, most particularly when they are the results of experiments designed on the basis of the theory itself, provides evidential support for the theory.

But that has confusedly misunderstood as confirmation of the theory as a whole in a way that raises its probability above its initial very low plausibility. What is confirmed are certain empirical consequences, and we are right to rely ever more on the theory, in our decisions and empirical predictions, as this support increases.

The name of the game is not confirmation but credentialing and empirical grounding.

APPENDIX

It is regrettable that discussions of confirmation give so often the impression of faith in the freakonomics slogan, that A RISING TIDE LIFTS ALL BOATS.

It just isn’t so.

Confirmation is more familiarly presented as due to conditionalization on new evidence, so let’s recast the argument in that form. The following diagram will illustrate this, with the same conclusion that the probability of the initial postulate does not change when the new evidence achieves relevance only because of the other parts of the theory.

Explanation: Proposition A is the initial postulate, and proposition B is what will eventually be cited as evidence. However, A by itself is still too uninformative to be testable at all.

The theory is extended by adding hypothesis H to A, and the more informative theory does allow for the design of a test. The test result is that proposition B is true.

The function q is the prior probability function. The size of the areas labeled A, B, H in the diagram represent their prior probabilities — notice that A and B are independent as far as the prior probability is concerned.

The function Q is the posterior probability, which is q conditionalized on the new evidence B.

The increase in probability of the conjunction (A & H) shows that the evidence confirms the theory taken as a whole. But the probability of A does not increase: Q(A) = q(A). The theory as a whole was confirmed only because its empirical consequence H was confirmed, and this ‘rising tide’ did not ‘lift the boat’ of the initial flamboyant postulate that gave the theory its name.

Tag: evidence

Evidential support versus confirmation

Subjective Probability and a Puzzle about Theory Confirmation