deontic logic

What Could Be the Most Basic Logic?

December 25, 2025December 25, 2025 Bas van Fraassen1 Comment

It was only in the 19^th century that alternatives to Euclidean geometry appeared. What was to be respected as the most basic geometry for the physical sciences: Euclidean, non-Euclidean with constant curvature, projective? Frege, Poincare, Russell, and Whitehead were, to various degrees, on the conservative side on this question.>^[1]

In the 20^th, alternatives to classical logic appeared, even as it was being created in its present form. First Intuitionistic logic, then quantum logic, and then relevant and paraconsistent logics, each with a special claim be more basic, more general in its applicability, than classical logic.

Conservative voices were certainly heard. John Burgess told his seminars “Heretics in logic should be hissed away!”. David Lewis described relevant and paraconsistent logic as logic for equivocators. The other side was not quiet. Just as Hans Reichenbach gave a story of coherent experience in a non-Euclidean space, so Graham Priest wrote a story of characters remaining seemingly coherent throughout a self-contradictory experience.

Unlike in the case of Euclidean geometry, the alternatives offered for propositional logic have all been weaker than classical logic. So how weak can we go? What is weaker, but still sufficiently strong, to qualify as “the” logic, logic simpliciter?

I am very attracted to the idea that a certain subclassical logic (FDE) has a better claim than classical logic to be “the” logic, the most basic logic. It is well studied, and would be quite easy to teach as a first logic class. Beall (2018) provides relevant arguments here – the arguments are substantial, and deserve discussion. But I propose to reflect on what the question involves, how it is to be understood, from my own point of view, to say why I find FDE attractive, and what open questions I still have.

1. A case for FDE

The question what is the most basic logic sounds factual, but I cannot see how it could be. However, a normative claim of the form

Logic L is the weakest logic to be respected in the formulation of empirical or abstract theories

seems to make good sense. We had the historical precedent of Hilary Putnam’s claiming this for quantum logic. I will come back to that claim below, but I see good reasons to say that FDE is a much better candidate.

2. Starting a case for FDE

FDE has no theorems. FDE is just the FDE consequence relation, the relation originally called tautological entailment, and FDE recognizes no tautologies. Let us call a logic truly simple if it has no theorems.

To be clear: I take L to be a logic only if it is a closure operator on the set of sentences of a particular syntax. The members of L(X) are the consequences of X in L, or the L-consequences of X; they are also called the sentences that X entails in L. A sentence A is a theorem of L iff A is a member of L(X) for all X. The reason why FDE has no theorems is that it meets the variable-sharing requirement: that is to say, B is an L-consequence of A only there is an atomic sentence that is a component of both B and A.

So the initial case for FDE can be this: it is truly simple, as it must be, because

logic does not bring us truths, it is the neutral arbiter for reasoning and argumentation, and supplies no answers of its own.

To assess this case we need a clear notion of what counts as a logic (beyond its being a closure operator), and what counts as supplying answers. If I answered someone’s question with “Maybe so and maybe not”, she might well say that I have not told her anything. But is that literally true? A. N. Prior once made a little joke, “What’s all the fuss about Excluded Middle? Either it is true or it is not!”. We would have laughed less if there had been no Intuitionistic logic.

3. Allowance for pluralism

My colleague Mark Johnston like to say that the big lesson of 20^th century philosophy was that nothing reduces to anything else. In philosophy of science pluralism, the denial that for every scientific theory there is a reduction to physics, has been having a good deal of play.

As I mentioned, FDE’s notable feature is the variable-sharing condition for entailment. If A and B have no atomic sentences in common, then A does not entail B in FDE. So to formulate two theories that are logically entirely independent, choose two disjoint subsets of the atomic sentences of the language. Within FDE, theories which are formulated in the resulting disjoint sublanguages will lack any connection whatsoever.

4. Could FDE be a little too weak?

The most conservative extension, it seems to me, would be to add the falsum, ⊥. It’s a common impression that adding this as a logical sign, with the stipulation that all sentences are consequences of ⊥, is cost-less.

But if we added it to FDE semantics with the stipulation that ⊥ is false and never true, on all interpretations, then we get a tautology after all: ~⊥. The corresponding logic, call it FDE⁺, then has ~ ⊥ as a theorem. So FDE⁺ is not truly simple, it fails the above criterion for being “the” logic. Despite that common impression, it is stronger than FDE, although the addition looks at once minimal and important. Is FDE missing out on too much?

How should we think of FDE⁺?

Option one is to say that ⊥, a propositional constant, is a substantive statement, that adding it is like adding “Snow is white”, so its addition is simply the creation of a theory of FDE.

Option two is to say that FDE⁺ is a mixed logic, not a pure logic. The criterion I would propose for this option is this:

A logic L defined on a syntax X is pure if and only if every syntactic category except that of the syncategoremata (the logical and punctuation signs) is subject to the rule of substitution.

So for example, in FDE the only relevant category is the sentences, and if any premises X entails A, in FDE, then any systematic substitution of sentences for atomic sentences in X entails the corresponding substitution in A.

But in FDE⁺ substitution for atomic sentence ⊥ does not preserve entailment in general. Hence FDE is a pure logic, and FDE⁺ is not.

The two options are not exclusive. By the usual definition, a theory of logic L is a set of sentences closed under entailment in L. So the set of theorems of FDE⁺ is a theory of FDE. However, it is a theory of a very special sort, not like the sort of theory that takes the third atomic sentence (which happens to be “Snow is white”) as its axiom.

Open question: how could we spell out this difference between these two sorts of theories?

5. Might FDE be too strong?

FDE is weak compared to classical logic, but not very weak. What about challenges to FDE as too strong?

It seems to me that any response to such a challenge would have be to argue that a notion of consequence weaker than FDE would be at best a closure operator of logical interest. But the distinction cannot be empty or a matter of fiat.

Distributivity

The first challenge to classical logic that is also a challenge to FDE came from Birkhoff and von Neumann, and was to distributivity. They introduced quantum logic, and at one point Hilary Putnam championed that as candidate for “the” logic. Putnam’s arguments did not fare well.^[2]

But there are simpler examples that mimic quantum logic in the relevant respect.

Logic of approximate value-attributions

Let the propositions (which sentences can take as semantic content) be the couples [m, E], with E an interval of real numbers – to be read as “the quantity in question (m) has a value in E”.

The empty set 𝜙 is counted as an interval. The operations on these propositions are defined:

[m, E] ∧ [m, F] = [m, E ∩ F]

[m, E] v [m, F] = [m, E Θ F],

where E Θ F the least interval that contains E ∪ F

Then if E, F, G are the disjoint intervals (0.3, 0.7), [0, 0.3], and [0.7, 1],

[m, E] ∧ ([m, F] v [m, G]) = [m, E] ∧ ([ m, [0,1]] = [m, E]

([m, E] ∧ ([m, F]) v ([m, E] ∧ ([m, G]) = [m, 𝜙]

which violates distributivity.

This looks like a good challenge to distributivity if the little language I described is a good part of our natural language, and if it can be said to have a logic of its own.

The open question:

if we can isolate any identifiable fragment of natural language and show that taken in and by itself, it has a logical structure that violates a certain principle, must “the” logic, the basic logic, then lack that principle?

Closure and conflict

We get a different, more radical, challenge from deontic logic. In certain deontic logics there is allowance for conflicting obligations. Suppose an agent is obliged to do X and also obliged to refrain from doing X, for reasons that cannot be reconciled. By what logical principles do these obligations imply further obligations? At first blush, if doing X requires doing something else, then he is obliged to do that as well, and similarly for what ~X requires. But he cannot be obliged to both do and refrain from doing X: ought implies can.

Accordingly, Ali Farjami introduced the Up operator. It is defined parasitic on classical logic: a set X is closed under Up exactly if X contains the classical logical consequences of each of its members. For such an agent, caught up in moral conflict, the set of obligations he has is Up-closed, but not classical-logic closed.

If we took Up to be a logic, then it would be a logic in which premises A, B do not entail (A & B). Thus FDE has a principle which is violated in this context.

To head off this challenge one reposte might be that in deontic logic this sort of logical closure applies within the scope of a prefix. The analogy to draw on may be with prefixes like “In Greek mythology …”, “In Heinlein’s All You Zombies …”.

Another reposte can be that FDE offers its own response to the person in irresolvable moral conflict. He could accept that the set of statements A such that he is obliged to see to it that A, is an FDE theory, not a classical theory. Then he could say: “I am obliged to see to it that A, and also that ~A, and also that (A & ~A). But that does not mean that anything goes, I have landed in a moral conflict, but not in a moral black hole.”

Deontic logic and motivation from ethical dilemmas only provide the origin for the challenge, and may be disputed. Those aside, we still have a challenge to meet.

We have here another departure from both classical logic and FDE in and identifiable fragment of natural language. So we have to consider the challenge abstractly as well. And it can be applied directly to FDE.

Up is a closure operator on sets of sentences, just as is any logic. Indeed, if C is any closure operator on sets of sentences then the operator

C^u: C^u(X) = ∪{C({A}): A in X}

is also a closure operator thereon. (See Appendix.)

So we can also ask about FDE^u. Is it a better candidate to be “the” logic?

FDE^u is weaker than FDE, and it is both pure and truly simple. But it sounds outrageous, that logic should lack the rule of conjunction introduction!

6. Coda

We could give up and just say: for any language game that could be played there is a logic – that is all.

But a normative claim of form

Logic L is the weakest logic to be respected in the formulation of empirical or abstract theories

refers to things of real life importance. We are not talking about just any language game.

Last open question: if we focus on the general concept of empirical and abstract theories, can we find constraints on how strong that weakest logic has to be?

FDE is both pure and truly simple. Among the well-worked out, well studied, and widely applicable logics that we already have, it is the only one that is both pure and truly simple. That is the best case I can make for it so far.

7. APPENDIX

An operator C on a set X is a closure operator iff it maps subsets of X to subsets of X such that:

X ⊆ C(X)
CC(X) = C(X)
If X ⊆ Y then C(X) ⊆ C(Y)

Definition. C^u(X) = ∪{C({A}): A in X}.

Proof that C^u is a closure operator:

X ⊆ C^u(X). For if A is in X, then A is in C({A}), hence in C^u(X).
C^uC^u (X) = C^u(X). Right to left follows from the preceding. Suppose A is in C^uC^u (X). Then there is a member B of C^u(X) such that A is in C({B}), and a member E of X such that B is in C({E}). Therefore A is in CC({E}). But CC({E}) = C({E}), so A is in C^u(X).
If X ⊆ Y then C^u(X) ⊆ C^u(Y). For suppose X ⊆ Y. Then {C({A}): A in X} ⊆ {C({A}): A in Y}, so C^u(X) ⊆ C^u(Y).

8. REFERENCES

Beall, Jc. (2018) “The Simple Argument for Subclassical Logic”. Philosophical Issues.

Cook, Roy T. (2018) “Logic, Counterexamples, and Translation”. Pp. 17- 43 in Geoffrey Hellman and Roy T. Cook (Eds.) (2018) Hilary Putnam on Logic and Mathematics. Springer.

Hellman, Geoffrey (1980). “Quantum logic and meaning”. Proceedings of the Philosophy of Science Association 2: 493–511.

Putnam, Hilary (1968) “Is Logic Empirical” Pp. 216-241 in Cohen, R. and Wartofsky, M. (Eds.). (1968). Boston studies in the philosophy of science (Vol. 5). Dordrecht. Reprinted as “The logic of quantum mechanics”. Pp. 174–197 in Putnam, H. (1975). Mathematics, matter, and method: Philosophical papers (Vol. I). Cambridge.

Russell, Bertrand (1897) An Essay on the Foundations of Geometry. Cambridge.

NOTES

^[1] For example, Russell concluded that the choice between Euclidean and non-Euclidean geometries is empirical, but spaces that lack constant curvature “we found logically unsound and impossible to know, and therefore to be condemned a priori (Russell 1897: 118).

^[2] See Hellman (1980) and Cook (2018) especially for critical examination of Putnam’s argument.

Truthmaker semantics for the logic of imperatives

August 28, 2024 Bas van FraassenLeave a comment

Seminal text: Nicholas Rescher, The Logic of Commands. London: 1966

Imperatives: the three-fold pattern 1
Denoting imperatives 2
Identifying imperatives through their truthmakers 2
Entailment and logical combinations of imperatives 3
Starting truthmaker semantics: the events. 4
Event structures 4
The language, imperatives, and truthmakers 5
Logic of imperatives 6
APPENDIX. Definitions and proofs 7

In deontic logic there was a sea change when imperatives were construed as default rules (Horty, Reasons as Defaults: 2012). The agent is conceived as situated in a factual situation but subject to a number of ‘imperatives’ or ‘commands’.

Imperatives can be expressed in many ways. Exclamation marks, as in “Don’t eat with your fingers!”, may do, but are not required. Adapting one of Horty’s examples, we find in a book of etiquette:

One does not eat food with one’s fingers
Asparagus is eaten with one’s fingers

These are declarative sentences. But in this context they encode defeasible commands, default rules. Reading the book of etiquette, the context in question, we understand the conditions in which the indicated actions are mandated, and the relevant alternatives that would constitute non-compliance.

In this form of deontic logic, what ought to be the case in a situation is then based on the facts there plus the satisfiable combinations of commands in force.^[1]

1. Imperatives: the three-fold pattern

Imperatives have a three-fold pattern for achievement or lack thereof:

Success: required action carried out properly
Failure: required action not carried out properly or not at all
Moot: condition for required action is absent

In the first example above, the case will be ‘moot’ if there is no food, or if you are not eating. Success occurs if there is food and it is not eaten with the fingers, Failure if there is food and it is eaten with the fingers.

Whenever this pattern applies, we can think of that task as having to be carried out in response to the corresponding imperative. There are many examples that can be placed in this form. For example, suppose you buy a conditional bet on Spectacular Bid to win in the Kentucky Derby. Doing so imposes an imperative on the bookie. He is obligated to pay off if Spectacular Bid wins, allowed to keep the money if she loses, and must give the money back if she does not run.

2. Denoting imperatives

An imperative may be identified in the form ‘When A is the case, see to it properly that B’. This way of identifying the imperative specifies just two elements of the three-fold pattern, Success and (the opposite of) Moot.

But the opposite of Moot is just the disjunction of the two contraries in which the condition is present. Therefore it is equally apt to represent the imperative by a couple of two contraries, marking Success and Failure. Doing so gives us a better perspective on the structure of imperatives and their relation to ‘ought’ statements.

So I propose to identify an imperative with an ordered pair of propositions <X, Y>, in which X and Y are contraries. Intuitively they correspond respectively to Success (and not Moot), and Failure (and not Moot).

3. Identifying imperatives through their truthmakers

Our examples point quite clearly to a view of imperatives that goes beyond truth conditions of the identifying propositions. What makes for success or failure, what makes for the truth of the statement that the imperative has been met or not met, are specific events.

That Spectacular Bid wins, or that you close the door when I asked you to, are specific facts or events which spell success. That I eat the asparagus with a fork is a distinct event which spells a failure of table etiquette.

Consider the command

(*) If A see to it that B!

as identified by its two contraries, Success and Failure. For each there is a class of (possible) events which ‘terminate’ the command, one way or the other.

The statement “Spectacular Bid wins” states that a certain event occurs, and encodes a success for the bookie’s client. The statement that encodes Failure is not “Spectacular Bid does not win”. Rather it is “Spectacular Bid runs and does not win”, which is, for this particular imperative the relevant contrary.

To symbolize this identification of imperatives let us denote as <X| the sets of events that make X true, and as |X> the set of events that make the relevant contrary (Failure) true.^[2] The imperative in question is then identified by an ordered couple of two sets of events, namely (<X|, |X>). I will abbreviate that to <X>.

In (*), <X> is the imperative to do B if A is the case, so X = the statement that (A and it is seen to that B), which is made true by all and only the events in set <X|. Its relevant contrary in this particular imperative is the statement that (A but it is not seen to that B), and that relevant contrary is whatever it is that is made true by all and only the events in set |X>.

4. Entailment and logical combinations of imperatives

There is an obvious sense in which E, “Close the door and open the window!” entails F, “Close the door!” Success for E entails success for F. But that is not all. Failure for F entails failure for E. The latter does not follow automatically from the former, if there is a substantial Moot condition: not winning the Derby does not, as such, imply losing.

So entailment between imperatives involves two ‘logical’ implications, going in opposite directions, and we can define:

Definition. Imperative A entails imperative B exactly if <A| ⊆ <B| and |B> ⊆ |A>.

“Open the door!” is a ‘strong’ contrary to “Close the door!”. There is a weaker contrary imperative: if someone looks like he is about to close the door, you may command “Do not close the door!”.

Negation. In the logic of statements, the contradictory is precisely the logically weakest contrary. For example, yellow is contrary to red and so is blue, but to be simply not red is to be either yellow or blue or … and so forth.

So I propose as the analogue to negation that we introduce

<┐A>: <┐A| = |A> and |┐A> = <A|

Whatever makes ┐A true is what makes A false, and vice versa. Here the symbol “┐” does not stand for the usual negation of a statements, because imperatives generally have significant, substantial conditions. The relevant contrary to Success is not its logical contradictory (that would be: either Failure or Moot) but Failure (which implies not-Moot), and that is whatever counts as Failure for the particular imperative in question.

Conjunction. “Close the door and open the window” we can surely symbolize as <A & B>. Success means success for both. In addition, failure means failure for one or the other or both. So there is no great distance between conjunction of Success statements and the ‘meet’ operation on imperatives:

<A & B>: <A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>.

Disjunction. Similarly, dually, for disjunction and the ‘join’ operation:

We can already see that some familiar logical relations are making an appearance.

[1] <A & B> entails <A>, while <A> entails <A v B>.

For example, <A & B| ⊆ <A| and |A> ⊆ |A & B>.

(All proofs will be provided in the Appendix.)

We could go a bit further with this. But answers to the really interesting questions will depend on the underlying structure of events or facts, that is, of the truthmakers.

5. Starting truthmaker semantics: the events.

Events combine into larger events, with an analogy to conjunction of statements. So the events form a ‘meet’ semilattice. Important are the simple events:

Postulate: Each event is a unique finite combination of simple events.

Is it reasonable to postulate this unique decomposability into simple events?

At least, it is not egregious. Think of how we specify a sample space for probability functions: each measurable event is a subset of the space. The points of the space may have weights that sum up to the measure of the event of which they are the members. Two events are identical exactly if they have the same members.

In any case, the idea of truthmakers is precisely to have extra structure not available in possible worlds semantics.

Combination we can conceive of as a ‘meet’ operation. Besides combining, we need an operation to identify contraries among events, in order to specify Success and Failure of imperatives.

Definition. A event structure is a quadruple E = <E, E0, ., ° >, where E is a non-empty set, . is a binary operation on E, E0 is a non-empty subset of E, and ° is a unary operation on E0, such that:

° is an involution: if a is in E0 then a° ≠ a and a°° = a
. is associative, commutative, idempotent (a ‘meet’ operator)
If e and e’ are elements of E then there are elements a_1, …, a_k,b_1, …, b_mof E0 such that e = a₁… a_k, and e’=b₁…b_m and e = e’ if and only if { a₁, …, a_k}= {b₁, …, b_m}

This last clause implies along the way that if e is an element of E then there is a set a₁, …, a_n of elements of E0 such that e = a₁ … a_n. That is part, but only part, of what the Postulate demands, and would not by itself imply unique decomposability.

The involution operates solely on simple events. A particular imperative could have a simple event b to identify Success; in that case simple event b° will be identify its Failure.

6. Event structures

The following definitions and remarks refer to such an event structure E.

Definition. e ≤ e’ if and only if there is an event f such that e’.f = e.

Analogy: a conjunction implies its conjuncts, and if A implies B then A is logically equivalent to (A & C) for some sentence C.

The definition is not the standard one, so we need to verify that it does give us a partial order, fitting with the meet operator.

[2] The relation ≤ is a partial ordering, and e.f is the glb of e and f.

That is, we have the familiar semilattice laws: e.g. if e ≤ e’ and f is any other event then f.e ≤ e’.

So <E, ., ≤ > is a meet semilattice. Note also that if a and b are simple events then a ≤ b only if a = b. For if b.f = a, the Postulate implies that b = f = a.

So far we have a relation of contrariety for simple events only. For events in general we need to define a general contrariness relationship.

Definition. Event e is contrary to event e’ if and only if there is an event a in E0 such that e ≤ a and e’ ≤ a° .

Contrariety is symmetric because a°° = a.

At this point we can see that the logic we are after will not be classical. For contrariety is not irreflexive.

That is because (a.a°) ≤ a and (a.a°) ≤ a°, so (a.a°) is contrary to itself. But (a.a°) is not the bottom of the semilattice. If a, a°, and b are distinct simple events then it is not the case that (a.a°) ≤ b. For if b.f = a.a° and f = a₁ … a_n then the Postulate requires {b, a_1, …, a_n} = {a, a°} so either b = a or b = a° .

It is tempting to get rid of this non-classical feature. Just reducing modulo some equivalence may erase the distinction between those impossible events, a.a° and b.b° . Such events can never occur anyway.

But there are two reasons not to do so. The first is that the history of deontic logic has run on puzzles and paradoxes that involve apparent self-contradictions. The second is more general. We don’t know what new puzzles may appear, whether about imperatives or related topics, but we hope to have resources to represent whatever puzzling situation we encounter. Erasing distinctions reduces our resources, and why should we do that?

7. The language, imperatives, and truthmakers

More formally now, let us introduce a language, and call it L_IMP. Its syntax is just the usual sentential logic syntax (atomic sentences, &, v, ┐). The atomic sentences will in a specific application include sentences in natural language, such as ‘”One does not eat with one’s fingers”. The interpretations will treat those sentences not as statements of fact but as encoding imperatives. In each case, the interpretation will supply what a context (such as a book of etiquette) supplies to set up the coding.

An interpretation of language L_IMP in event structure E = <E, E0, ., ° > begins with a function f that assigns a specific event to each atomic sentence in each situation. Then there are two functions, < | and | >, which assign sets of truth-makers to each sentence:

If A is atomic and a = f(A) then <A| = {e in E: e ≤ a} and |A> = {e in E: e ≤ a°}.
<┐A| = |A> and |┐A> = <A|
<A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>
<A v B| = <A| ∪ <B|, |A v B> = |A> ∩ |B>

Definition. A set X of events is downward closed iff for all e, e’ in E, if e ≤ e’ and e’ is in X then e is in X.

[3] For all sentences A, <A| and |A> are downward closed sets.

Now we can also show that our connector ┐, introduced to identify the weakest contrary to a given imperative, corresponds (as it should) to a definable operation on sets of events.

Definition. If X ⊆ E then X^⊥ = {e: e is contrary to all elements of X}.

I will call X^⊥ the contrast (or contrast class) of X.

Lemma. X^⊥ is downward closed.

That is so even if X itself is not downward closed. For suppose that f is in X^⊥. Then for all members e of X there is a simple event a such that f ≤ a and e ≤ a°. Thus for any event g, also g.f.e ≤ a while e ≤ a°. Therefore g.f is also in X^⊥.

[4] For all sentences A, <┐A| = |A> = <A|^⊥ and |┐A> = <A| = |A>^⊥ .

The proof depends De Morgan’s laws for downward closed sets of events:

Lemma. If X and Y are downward closed sets of events then

(X ∩ Y)^⊥ = X^⊥ ∪ Y^⊥ and (X ∪ Y)^⊥ = X^⊥ ∩ Y^⊥.

In view of [4], there is therefore an operator on closed sets of events that corresponds to negation of imperatives:

Definition. If A is any sentence then <A>^⊥ = (<A|^⊥ , |A>^⊥ ).

[5] <A>^⊥ = <┐A>

This follows at once from [4] by this definition of the ^⊥ operator on imperatives.

8. Logic of imperatives

We will concentrate here, not on the connections between sentences A, but on connections between their semantic values <A>. These are the imperatives, imperative propositions if you like, and they form an algebra.

Recall the definition of entailment for imperatives. It will be convenient to have a symbol for this relationship:

Definition. <A> ⇒ exactly if <A| ⊆ <B| and |B> ⊆ |A>.

The following theorems introduce the logical principles that govern reasoning with imperatives.

[6] Entailment is transitive.

To have the remaining results in reader-friendly fashion, let’s just summarize them.

[7] – [11]

Meet.
- <A & B> ⇒ <A>,
- <A & B> ⇒ 
- If <X> ⇒ <A> and <X> ⇒ then <X> ⇒ <A & B>
Join.
- <A> ⇒ <A v B>
- ⇒ <A v B>
- If <A> ⇒ <X> and ⇒ <X> then <A v B> ⇒ <X>
Distribution: <A &(B v C)> ⇒ <(A & B) v (A & C)>.
Double Negation. <A> ⇒ < ┐ ┐ A> and < ┐ ┐ A> ⇒ <A>.
Involution. If <A> ⇒ then <┐B> ⇒ <┐A>.
De Morgan.
- < ┐ (A & B)> ⇒ < ┐A v ┐B> and vice versa
- < ┐ (A v B)> ⇒ < ┐A & ┐B> and vice versa.

COMMENTS. In order for these results to make proper sense, each of the connectors ┐, &, v needs to correspond to an operator on imperatives, modeled as couples of downward closed sets of events. This was shown in the previous section.

The logic of imperatives is not quite classical. We can sum up the above as follows:

The logic of imperatives mirrors FDE (logic of first degree entailment); the imperatives form a De Morgan algebra, that is, a distributive lattice with De Morgan negation.

APPENDIX. Definitions and proofs

Definition. Imperative A entails imperative B exactly if <A| ⊆ <B| and |B> ⊆ |A>.

[1] <A & B> entails <A>, and <A> entails <A v B>.

For <A & B| = <A| ∩ <B| ⊆ <A| while |A > ⊆ |A|> ∪ |B> = |A & B>. Similarly for the dual.

Postulate: each event is a unique finite combination of simple events.

° is an involution: a° ≠ a and a°° = a, if a is in E0
. is associative, commutative, idempotent (a ‘meet’ operation)
If e and e’ are elements of E then there are elements a_1, …, a_k,b_1, …, b_mof E0 such that e = a₁… a_k, and e’=b₁…b_m and e = e’ if and only if { a_1, …, a_k}= {b_1, …, b_m}

[2] The relation ≤ is a partial ordering, and the meet e.f of e and f is the glb of e and f.

For e ≤ e because e.e = e (reflexive), and if e = e’.f and e’ = e”.g then e = e”.f.g (transitive).

(Perhaps clearer: For if e = e’.f then e.g = e’.f.g, so if e ≤ e’ then e.g ≤ e’, for all events g.)

Concerning the glb:

First, e.f ≤ e because there is an element g such that e.f .g = e. g, namely g = f.

Secondly suppose e’ ≤ e, and e’ ≤ f. Then there are g and h such that e.g = e’ and f.h = e’. In that case e’ = g.h.f.e, and therefore e’ ≤ e.f.

Definition. Event e is contrary to event e’ if and only if there is an event a in E0 such that e ≤ a and e’ ≤ a° .

Contrariness is symmetric because a°° = a. But it is not irreflexive for (a.a°) ≤ a and (a.a°) ≤ a°.

Lemma 1. If a and b are simple events then a ≤ b only if a = b.

That is because decomposition into simple events is unique. For suppose that a.f = b. Then there are simple events c₁, …, c_k such that f = c₁….c_k and a.f = a. c₁, …, c_k = b, which implies that a = c₁ = … = c_k = b.

Interpretation of the imperatives expressed in language LIMP, in event structure E = = <E, E0, ., ° >, relative to function f from atomic sentences to simple events. Then there are two functions, < | and | >, which assign sets of truth-makers to each sentence:

If A is atomic and a = f(A) then <A| = {e in E: e ≤ a} and |A> = {e in E: e ≤ a° }.
<┐A| = |A> and |┐A> = <A|
<A & B| = <A| ∩ <B|, |A & B> = |A> ∪ |B>
<A v B| = <A| ∪ <B|, |A v B> = |A> ∩ |B>

Definition. A set X of events is downward closed iff for all e, e’ in E, if e ≤ e’ and e’ is in X then e is in X.

[3] For all sentences A, <A| and |A> are downward closed sets.

Hypothesis of induction: this is so for all sentences of length less than A.

Cases.

A is atomic. This follows from the first of the truth-maker clauses
A has form ┐B. Then <B| and |B> are downward closed, and these are respectively |┐A> and <┐A|.

A has the form (B & C) or (B & C). Here it follows from the fact that intersections and unions of downward closed sets are downward closed.

Definition. If X ⊆ E then X^⊥ = {e: e is contrary to all elements of X}

Lemma 2. X^⊥ is downward closed.

Suppose that e is in X^⊥. Then for all e’ in X, there is a simple event a such that e ≤ a and e’ ≤ a . This implies for any event f, that f.e ≤ a and e’ ≤ a . Hence f.e is also in X^⊥.

[4] For all sentences A, <┐A| = |A> = <A|^⊥ and |┐A> = <A| = |A>^⊥ .

Hypothesis of induction: If B is a sentence of length less than A then <┐B| = |B> = <B|^⊥ and |┐B> = <B| = |B>^⊥ .

Cases.

A is atomic, and f(A) = a. Then by the first truth-maker clause, all elements of |A> are contrary to all of <A|. Suppose next that e is contrary to all of <A|, so e is contrary to a, hence there is a simple event b such that a ≤ b and e ≤ b° . But then a = b, so e ≤ a° , hence e is in |A>. Similarly all elements of <A| are contrary to all elements of |A>, and the remaining argument is similar.
A has form ┐B. Then by hypothesis <┐B| = |B> = <B|^⊥ . And <┐┐B| = |┐B> by the truthmaker conditions, and |┐B> = <B|, and the hypothesis applies similarly to this.
A has form (B & C)

We prove first that <┐A| = |A> = <A|^⊥

<A| = <B| ∩ <C|, while <┐A| = |B & C> = |B> ∪ |C>. If e is in <┐A| then it is in |B> ∪ |C> so by hypothesis e is contrary either to all of <B| or to all of <C|, and hence to their intersection.

Suppose next that e is in <A|^⊥ = (<B| ∩ <C|)^⊥ . To prove that this is <┐A| = <┐(B & C)| = |B & C> = |B> ∪ |C> = <B|^⊥ ∪ <C|^⊥ it is required, and suffices, to prove the analogues to De Morgan’s Laws for downward closed sets. See Lemma below.

We prove secondly that |┐A> = <A| = |A>^⊥ . The argument is similar, with appeal to the same Lemma below.

(4) A has form (B v C). The argument is similar to case (3), with appeal to the same Lemma below.

Lemma 3. De Morgan’s Laws for event structures: If X and Y are downward closed sets of events then (X ∩ Y)^⊥ = X^⊥ ∪ Y^⊥ and (X ∪ Y)^⊥ = X^⊥ ∩ Y^⊥.

Suppose e is in X^⊥. Then e is contrary to all of X, hence to all of X ∩ Y, hence is in (X ∩ Y)^⊥. Similarly for e in Y^⊥. Therefore (X^⊥ ∪ Y^⊥ ) ⊆ (X ∩ Y)^⊥.

Suppose on the other hand that e is in (X ∩ Y)^⊥. Suppose additionally that e is not in X^⊥. We need to prove that e is in Y^⊥.

Let e’ be in X and not contrary to e. Then if e’’ is any member of Y, it follows that e’.e’’ is in X ∩ Y, since X and Y are both downward closed. Therefore e is contrary to e’.e’’. We need to prove that e is contrary to e”.

Let b be a simple event such that e ≤ b and e’.e” ≤ b°. By our postulate, e’ and e’’ have a unique decomposition into finite meets of simple events. So let e’ = a₁…a_k and e’’= c₁…c_m, so that e’.e” = a₁…a_k.c₁…c_m. Since e’.e” ≤ b°, there is an event g such that a₁…a_k.c₁…c_m = e’.e’’= g.b°. The decomposition is unique, so b° is one of the simple events a₁, …, a_k, c₁, …, c_m. Since e is not contrary to e’, it follows that none of a₁,…, a_k is b°. Therefore, for some j in {1, ..,m}, c_j = b°, and therefore there is an event h such that e” = h. b°, in other words, e” ≤ b°. Therefore e is contrary to e”.

So if e is not in X^⊥ then it is in Y^⊥, and hence in X^⊥ ∪ Y^⊥.

The argument for the dual equation is similar.

In view of the above, there is an operator on closed sets of events that corresponds to negation of imperatives:

Definition. If A is any sentence then <A>^⊥ = (<A|^⊥ , |A>^⊥ ).

[5] <A>^⊥ = <┐A>

(<A|^⊥ , |A>^⊥ ) = (<┐A|, |┐A>), in view of [4].

Definition. <A> ⇒ exactly if <A| ⊆ <B| and |B> ⊆ |A>.

The following theorems introduce the logical principles that govern reasoning with imperatives.

[6] Entailment of imperatives is transitive.

Suppose <A> ⇒ and ⇒ <C>. Then <A| ⊆ <B| and <B| ⊆ <C|, hence <A| ⊆ <C|. Similarly, |C> ⊆|A>.

[7] <A & B> ⇒ <A>, and if <X> ⇒ <A> and <X> ⇒ then <X> ⇒ <A & B>, Also <A> ⇒ <A v B>, and if <A> ⇒ <X> and ⇒ <X> then <A v B> ⇒ <X>

First, <A| ∩ <B| ⊆ <A| and |A> ⊆ |A> ∪ |B>, hence <A & B> ⇒ <A>.

Secondly, suppose that X is such that <X| ⊆ <A| and <X| ⊆ <B| while |A> ⊆ |X> and |B> ⊆ |X>. Then <X| ⊆<A| ∩ <B| = <A& B| while |A & B> = |A> ∪ |B> ⊆ |X>. Hence <X> ⇒ <A & B>.

The dual result for disjunction by similar argument.

[8] Distribution: <A &(B v C)> ⇒ <(A & B) v (A & C)>.

<A &(B v C)| = <A| ∩ <B v C| = <A| ∩ (<B| ∪ <C|) = [<A| ∩ <B| ] ∪ [<A| ∩ <C|)] = <(A & B) v (A & C|. Similarly for the other part.

[9] Double Negation: <A> ⇒ < ┐ ┐ A> and < ┐ ┐ A> ⇒ <A>.

< ┐ ┐ A| = |┐ A> = <A| and |┐ ┐ A> = <┐ A| = |A>

[10] Involution. If <A> ⇒ then <┐B> ⇒ <┐A>.

<┐B> ⇒ <┐A> exactly if <┐B| ⊆ <┐A|, i.e. |B> ⊆ |A>, and |┐A> ⊆ |┐B>, i.e. <A| ⊆ <B|. But that is exactly the case iff <A> ⇒

[11] De Morgan. < ┐ (A & B)> ⇒ < ┐A v ┐B> and vice versa, while < ┐ (A v B)> ⇒ < ┐A & ┐B> and vice versa.

< ┐ (A & B)| = |A & B> = |A> ∪ |B> = < ┐A| ∪ < ┐B| = < ┐A v ┐B|. Similarly for |┐(A & B> . Therefore < ┐ (A & B)> = < ┐A v ┐B>.

Similarly for the dual.

7. REFERENCES

Curry, Haskell B. (1963) Foundations of Mathematical Logic. New York: McGraw-Hill.

Lokhorst, Gert-Jan C. (1999) “Ernst Mally’s Deontik”. Notre Dame Journal of Formal Logic 40 : 273-282.

Mally, Ernst (1926) Grundgesetze des Sollens: Elemente der Logik des Willens. Graz: Leuschner und Lubensky

Rescher, Nicholas (1966) The Logic of Commands. London: Routledge and Kegan Paul

NOTES

^[1] Rescher traces this analysis of ‘ought’ statements to Ernst Malley (1926) who coined the name Deontik for his ‘logic of willing’. Since the logic of imperatives we arrive at here is non-classical, note that Lokhorst (1999) argues that Mally’s system is best formalized in relevant logic.

^[2] We can use Dirac’s names for them, “bra” and “ket”, with no reference to their original use.

Deontic logic, time, and 1876

November 2, 2021 Bas van FraassenLeave a comment

We use “ought” in two senses, evaluative (“things are not as they ought to be”) and hortatory (“you ought to do the best thing”). The latter is future-directed, and time entered deontic logic (with stit semantics) for that reason. But time brings much in train. What if you do what is the best thing in the short run, for tomorrow for example, and it precludes important options for the day after tomorrow? Or the day after that?

This is how infinity enters: a branching time, infinitely branching possible futures, with the outcomes of our choices. Our deliberation and decision making is inevitably short-sighted, considered sub specie aeternitatis. We can only see finitely many moves ahead. But that implies a danger: how do I form a policy that does not, with equal inevitability, lead me into an ultimately unsatisfying life?

Reflecting on this I remembered F. H. Bradley’s critique of Utilitarianism.

Frances Herbert Bradley, Ethical Studies (1876)

As a student I never liked ethics until I read Bradley. As a British Idealist he was intent on bringing to light all the contradictions in our experienced world; in ethics this led him to see an unresolvable conflict between the ideals of self-sacrifice and self-realization. Fascinating … but here I just want to focus on one little point, his criticism of Utilitarianism, which focused on moral deliberation over time.

The form of Utilitarianism Bradley confronts is, more or less, what is now typically described as rational preference based decision making, cost and benefit analysis, maximizing expected value. As he sees it, this form of reasoning leads inevitably to a sort of life to be regretted, such as the life of a miser who saves to become rich but can never stop saving, or of the businessman who works to make a million but can never stop pursuing the next million. In the exquisite prose of the British Idealists, which we cannot emulate today:

Happiness, in the meaning of always a little more and always a little less, is the stone of Sisyphus and the vessel of the Danaides — it is not heaven but hell. (Essay III)

Falling into this trap seems inevitable if we pursue a quantifiable value, and if this pursuit is not subject to any constraint, whether external or internal, independent of that value. Let’s make this concrete.

The Contra Costa game

To the literature about problems with infinity in decision-making, such as the St. Petersburg Paradox and the Pasadena Game, I propose to add this one, to illustrate Bradley’s argument.

A coin will be tossed as often as we like. If you enter into the game here is what will happen. If the first toss comes up heads, you have two options. The first is to accept $10, and the game stops for you. The second option is to stay in the game. If the second toss then comes up heads you may choose between accepting $100 or staying in the game. And so on: if the n^th toss came up heads, you can choose between accepting $10^m, where m is the number of tosses that have come up heads so far; or you can stay in the game. If the toss comes up tails the game ends, and the player who stayed in ( unlike in the St Petersburg game), ends up with nothing at all.

Suppose toss N has just come up heads. If you stay in you have a 50% chance of getting the option to accept 10^(N+1), which is ten times more than what you could get now. There is also a 50% chance of getting 0. So the expectation value of staying in equals 0 plus 0.5(10)(10^N) = 5 times the value of opting out.

Thus what you ought to do (if your rule is to maximize expected value and you look only one day ahead), as long as you are in the game, at every stage, if the toss came up heads, is to stay in. And the result is that you will never get anything at all: you are living a life of anxious expectation, never able to let go of this devilish ladder of fortune, until either you are out with nothing to show for it, or you go on forever with no no payoff ever.

It may be objected here that no casino could be in a position to offer this game, it could not set a high enough price for entry. That is what we usually say about the St. Petersburg game as well. But think about the real-life analogue. The person who sets out to make a million, and remains at every stage intent on making the next million, has no reason to think that the world cannot afford to offer this possibility. The price paid is the work involved in making money, which is gladly paid.

There was a writer who traded on his readers giving some credence to there being a source with unlimited means: Blaise Pascal.

Similarity to Pascal’s Wager

Here is how Pascal might have posed the problem of the Contra Costa game for the rational unbeliever:

Everyday God says “Repent now, and you shall have eternal bliss!”

Everyday the unbeliever responds in her/his heart “I can take one more day and repent tomorrow, that has a higher value!”

(a) The game ends when s/he dies, and s/he loses.

(b) s/he lives forever. With this policy, she has the fate of Barend Fokke, the Flying Dutchman.

Either way, s/he misses out on eternal bliss.

Is there help from long-term thinking?

The unfortunate player we have just been discussing has this flaw: s/he looks only one day ahead. That it is a day, does not matter: there is a fixed unit of time such that s/he looks ahead only that unit of time, in making her rational decision on the basis of expected value.

I did not eat a chocolate bar just now because it would ruin my appetite, and make dinner much less enjoyable. So I am not that naive Utilitarian agent who just looks one minute, or one hour, ahead. I forego the immediate gain for the sake of gain over a longer period.

But what is that longer period? If it is, say 2 hours, or 2 days, then I am after all that naive agent, with a different time scale, focused on gain in a finite future period. In the Contra Costa game this will not keep me from continuing forever: I will not take today’s prize. Suppose I reflect on the possibilities for the next two tosses of the coin, when the first N tosses have come up heads. The probability is 0.25 that I can get two more heads, and can then accept 10^(N + 2). There is also a 0.75 chance that I will gain zero. So the expected value of that scenario is 0.25(100)(10^N), or 25 times what I can get now. Thinking farther ahead increases the temptation, the incentive, to stay in the game.

What if I am an ideal long term thinker, who does not set a finite limit on his long term evaluations? The probability is zero that the coin will always come up heads. This is relevant for those ideal long term thinkers who take themselves to be immortal: they will rationally refuse to play. But these are either deceived (if all men are mortal) or at least negligibly rare.

Escape from the game: not by cost-benefit analysis

There may be an easy advice to give to the player: Do look beyond the immediate future! Choose some N, and decide not to go farther, no matter what. That is, decide that you will take the money at some stage either before or when there are N heads in a row.

But how is this choice to be made? The expectation value when you make this choice to be N, is 0/2 + 10/4 + 100/8 + … +10^N/(N+1). That is less than for the choice of N+1. So if you choose N, you are not choosing to maximize expected value. It goes against the principle of rational cost-benefit analysis.

The tree of possible futures in this game is a finitely branching tree which has many finite branches and an infinite branch. The latter, the fate of Bradley’s naive but immortal agent, is clearly to be avoided (we ought not to do that!). But a choice among the others on the basis of their value is not possible: for every value seen there, there is one with greater value.

There is no question that we must applaud those who at some point take their winnings and rest content. (“Take the money and run!”, Woody Allen — and how did that work for you?) We must applaud them although that choice is not ratifiable by value-preference based decision making. So if there is to be an escape, we have to tell the agent to bring with her some constraint of her own, which overrides the maxim to maximize expected value. What could that be?

Escape from the game: projects and goals

What follows is a suggestion, that I think deserves to be explored when developing deontic logic. It is not my suggestion, but one I heard long ago. (Perhaps only in conversation, I am not sure.)

Glenn Shafer proposed, at one time, that practical reasoning should be conceived of as in the first instance goal-directed. Shafer was pointing to a fact about the phenomenology of practical deliberation: it is not realistic to depict us as cost-and-benefitters, we set our goals and deliberate only within the span of possibilities left open by our goals.

(What about the goal-setting activity, we may ask? A specific goal may be set as the outcome of a deliberation, which took place within the limits set by previous goals. There is no beginning, we are thrown into a life in which we find basic goals already set. Il n’y a pas dehors du … )

I am saving for a holiday in Hawaii next winter. To have that holiday is my goal. The actual value to me of this holiday, if it happens, will depend on many factors (weather, companions, …) but these factors do not figure in the identity of the goal. (They might have figured, in some way, in my goal-setting).

This goal then constrains what I ought to do meanwhile. Among choices I face along the way, it will delete options that conflict with my going to Hawaii next winter. And if my choices get to the point where only one more move is necessary (getting on the plane …) it will prevent me from self-sabotage. For it would be self-sabotage (given the goal I have) to be looking around at that point and considering alternatives, however amazingly attractive they may be just then.

And it is part of the concept of having a goal that there is a stopping point: when the goal is reached, it is not foregone in favor of a suddenly glimpsed pretty face or chance at a bit of easy money.

So in the Contra Costa game this could be the goal of gaining $1000 (perhaps exactly what I need to pay off my loans, or to buy my wife a necklace for her birthday). That implies that I will accept $1000 and end the game if the coin comes up heads three times in a row. I may lose of course, but what I will not do after three heads in a row is to take a chance on getting $10,000. True, I would have a 50% chance of getting 10 times more, but I have reached my goal, rest content, and do not start on a life of Sisyphus.

There are of course less strictly fashioned constraints: we could call this one a Shafer Goal, and agree that there are also defeasible goals, that would need more sophisticated modeling.

What is crucially important is to recognize the necessary independence, autonomy, externality of the constraint (even though set by the actor herself). For if the choice of constraint itself has to be based on value-preference expectation reasoning, we have not escaped the game at all, we have just found ourselves in the same game on another level.

If the constraint takes the form of a goal I set myself, this must be modeled as an independent imperative or default rule, inserted at a different place. It must be, that is to say, another heart’s command not assimilable in value-preference based reasoning.

Deontic logic: value-rankings

January 15, 2021July 18, 2021 Bas van FraassenLeave a comment

The historical opening chapter of the Handbook of Deontic Logic and Normative Systems shows that, in various forms, this has been a typical way to connect ‘ought’ statements with values:

[O] It ought to be that A if and only if it is better that A than that ~A

as well as

[Cond O] It ought to be that A, on supposition that B if and only if it is better that (B & A) than that (B & ~A)

But in addition, deontic logics typically include the law that carries logical implication into the derivation of ‘ought’ statements:

[IMP] If A implies B then (It ought to be that A) implies (It ought to be that B)

(and the similar law for conditional ‘ought’ statements), important to keep the logic within the range of normal modal logics.

But do [O] and [IMP] go well together? That depends on the character of the value ranking which defines the ‘better than’ relation among propositions. Specifically, it requires that

[MON] If A implies B, and A is better than ~A, then B is better than ~B.

Problem: I will give examples below of ‘better than’ relations which do have property MON but which are intuitively unsatisfactory. But a ranking by expectation value does not have property MON.

Ranking by expectation value does not have MON: For example, a bank robber is confronted by the police. His best option (by expectation value) is to surrender. What about the option to (surrender or resist arrest)? This is America! If he resists arrest he will likely be shot. That lowers the expectation value considerably. (Reminiscent of Ross’ paradox, also about IMP.)

Solution: There is something right about [O] and [CondO], namely that value rankings have an important role to play in the understanding of ‘ought’ statements. But there is also something wrong about [O] and [CondO], namely that they presuppose that it is just, and only, value rankings that must determine the status of ‘ought’ statements.

But let me first give examples of rankings that do have MON and say why I find them unsatisfactory. In my own essay on deontic logic as a normal modal logic (1972) I gave this definition:

Ought(A) is true exactly if opting for ~A precludes the attainment of some value which it is possible to attain if one opts for A

or less informally,

Ought(A) is true in possible world h exactly if, there are worlds satisfying A which have a higher value than any worlds that satisfy ~A.

Very unsatisfactory! Today I opted not to buy a lottery ticket, thereby precluding a million dollar windfall (larger than anything I could get otherwise) and so I was wrong. I ought to have bought that ticket! As gamblers say, when you talk about prudence, “Yes, but what if you win!” Sorry, gamblers — this is not a good guide to life …

Jeff Horty offered a more sophisticated formulation in his 2019 paper (p. 78, the Evaluation Rule) as his explication of the Meinong/Chisholm analysis, which would in a normal modal logic context amount to:

Ought(A) is true in world h exactly if A is true in all worlds h’ possible relative to h, such that there is no world h” which satisfies ~A and has a value higher than h’.

Except for the relativization of possibility, this is like the preceding. Horty rightly rejects this as unsatisfactory, using the example of a forced choice between two gambles which has the same expectation value, but of which one carries no risk of loss. (One has outcomes 10 and 0, the other has only outcome 5 with certainty.) It is certainly not warranted to say that we ought always to make the gamble with the higher prize but higher risk.

There are surely other value rankings to to try, and I thought of this one:

Ought(A) is true in world h exactly if there is a one-to-one function f mapping the worlds that satisfy ~A into the worlds that satisfy A, such that for all worlds h in the domain of f the value h is less than the value of f(h).

This one too has property MON. Informally put, it means that whatever outcome you get if you opt for ~A, you realize you might have done better by choosing for A.

But imagine: gamble ~ A has with certainty one of the outcomes 5, 7, or 9 dollars, while gamble A has with certainty one of the outcomes 1, 10, 12, 14 dollars. However, to make gamble A you have to buy a ticket for $4. So your net outcomes for A are loss of $3, or win of 6, 8, 10. Clearly by the above principle you should take gamble A, for 5 < 6 < 7 <8 < 9 < 10. But is that really the right thing to do? If all the outcomes are equally likely then ~A has expectation value (21/3) and A has expectation value (21/4), which is less.

In previous posts I have discussed how Horty goes beyond this.

Now I just want to explain how the use of expectation value ranking works well with what I proposed some weeks ago in the post Deontic logic: two paradoxes” (which I gave a more precise formulation in the next post, “Deontic logic: Horty’s new examples”.) By “works well” I mean that the principle [IMP] is valid.

My proposal was that in setting up the framework for deontic logic, , we need to include both imperatives and values. So I envisage the agent as first of all recognizing the imperatives in force in his situation (‘if you have sinned, repent!’). The agent’s next step is to take account of the satisfaction regions for those imperatives (or better, maximally consistent sets of them). Then the value-ranking is applied to those satisfaction regions, and the ones that count are the ones that get highest value (the optimal regions). Next:

It ought to be that A if and only if there is an optimal region that implies A.

(This can be extended to conditional oughts in the way Horty does: go look at the alternative situation in which the agent has the condition added to his knowledge.)

When entered at this point, it does not matter whether the ranking has property MON. For what ever the ranking is, if an optimal region is part of A, and A is part of B, then an optimal region is part of B.

The story for choices, decisions and action planning is similar. It is not that the agent ought to do what is best, but rather that he has to make a best choice (the moral of Horty 2019). Suppose it is already settled that I will gamble, and I have a choice between several gambles. Now what ought to be the case (about what I do, about my future) is whatever is implied by my making a best choice. And I propose that the best choices are those which are represented by propositions (the choices themselves, not the possible outcomes of those choices) which have highest expectation value.

Deontic logic: Horty’s gambles (2)

January 6, 2021 Bas van FraassenLeave a comment

In the second part of his 2019 paper Horty argues that there is a need to integrate epistemic logic with deontic logic, for “ought” statements often have a sense in which their truth-value depends in part on the agent’s state of knowledge.

I agree entirely with his conclusion. But is the focus on knowledge not too strict? Subjectively it is hard to distinguish knowledge from certainty — and apart from that, when we don’t have certainty, we are still subject to the same norms. So I would like to suggest that rational opinion, in the form of the agent’s actual subjective probability, is what matters.

Here I will examine Horty’s additional examples of gambling situations with that in mind. I realize that this is not sufficient to demonstrate my contention, but it will show clearly how the intuitive examples look different through the eyes of this less traditional epistemology.

Horty’s figure 4 depicts the following situation: I pay 5 units to be offered one of two gambles X1, X2 on a coin toss. My options will be to bett Heads, to bet Tails, or Not To Gamble. But I will not know which gamble it is! You, the bookmaker will independently flip a coin to determine that, and not tell me the outcome. In the diagram shown here, X1 is the gamble on the left and X2 the gamble on the right.

On Horty’s initial analysis, if in actual fact I am offered X1 then I should bet Heads, since that has the best outcome. But as he says, rightly, I could not be faulted for not doing that, since I did not know whether I was being offered X1 or X2.

Even if the conclusion is the same, the situation looks different if the agent acts on the basis of the expectation values of the options available to him. The alternatives depicted in the diagram are equi-probable (we assume the coins are fair). So for the agent, who has paid 5 units, his net expectation value for betting Heads (in this situation where it is equally probable that he is betting in X1 or in X2) is the average of gaining 5 and losing 5. The expectation value is 0. Similarly for the option of betting Tails, and similarly for the option of Not Gambling: each has net expectation value 0. So in this situation it just is not true that the agent ought to take up any of these options — it is indifferent what he does.

Horty offers a second example, where the correct judgment is that I ought not to gamble, to show that his initial analysis failed to entail that. Here is the diagram, to be interpreted in the same way as above — the difference is in the value of the separate possible outcomes.

Reasoning by expectation value, the agent concludes that indeed she ought not to gamble. For by not gambling the payoff is 5 with certainty, while the expectation value of Betting Heads, or of Betting Tails, is 2.5.

So on this analysis as well we reach the right conclusion: the agent ought not to gamble.

Entirely in agreement with Horty is the conclusion that these situations are adequately represented only if we bring epistemology into play. What the agent ought to do is not to be equated with what it would objectively, in a God’s eye, be best for her to do. It is rather what she ought to do, given her cognitive/epistemic/doxastic situation in the world. But she cannot make rational gambling decisions in general if her knowledge (or certainty) is all she is allowed to take into account.

It would be instructive to think also about the case in which it is known that the coin has a bias, say that on each toss (inlcuding the hidden first toss) it will be three times as likely as not to land heads up. Knowledge will not be different, but betting behavior should.

Deontic logic: Horty’s gambles (1)

January 5, 2021 Bas van FraassenLeave a comment

In “Epistemic oughts in Stit Semantics” Horty’s main argument is that an epistemic logic must be integrated in a satisfactory deontic logic. This is needed in order to account for a sense of what an agent ought to do hinges on a role for knowledge (“epistemic oughts”).

That argument occupies the second part of his paper, and I hope to explore it in a later post. But the first part of the paper, which focuses on a general concept of what an agent ought to do (ought to see to) is interesting in itself, and crucial for what follows. I will limit myself here to that part.

I agree with a main conclusion reached there, which is that the required value ordering is not of the possible outcomes of action but of the choices open to the agent.

However, I have a problem with the specific ordering of choices that Horty defines, which it seems to me faces intuitive counterexamples. I will propose an alternative ordering principle.

At a given instant t an agent has a variety V(h, t) of possible futures in history h. I call V(h, t) the future cone of h at t. But certain choices {K, K’, …} are open to the agent there, and by means of a given choice K the agent may see to it that the possible futures will be constrained to be in a certain subset V(K, h, t) of V(h, t).

The different choices are represented by these subsets of V(h, t), which form a partition. Hence the following is well defined for histories in V(m): the choice made in history h at t is the set V(K, h, t) to which h belongs; call it CA(h, t), thinking of “CA” as standing for “actual choice”.

In the diagram K1 is the set of possible histories h1 and h2, and so CA(h1,t) = K1 = CA(h2, t). (Note well: I speak in terms of instants t of time, rather than Horty’s moments.

And the statement that the agent sees to it that A is true in in h at t exactly if A is true in all the possible futures of h at t that belong to the choice made in history h at t. Briefly put: CA(h, t) ⊆ A.

The Chisholm/Meinong analysis of what ought to be is precisely what it is maximally good to be the case. Thus, at a given time, it ought to be that A if A is the case in all the possible future whose value is maximal among them. So applied to a statement about action, that means: It ought to be that the agent sees to it that A is true in h at t exactly if all the histories in the choice made in history h at t are of maximal value. That is, if h is in CA(h, t) and h’ is in V(h, t) but outside CA(h, t) then h’ is no more valuable than h.

But this analysis is not correct, as Horty shows with two examples of gambles. In each case the target proposition is G: the agent gambles, identified with the set of possible histories in which the agent takes the offered gamble. This is identified with: the agent sees to it that G. Hence the two choices, K1 and K2, open to the agent in h at t are represented by the intersection of V(h, t) with G and with ~G respectively.

In the first example the point made is that according to the above analysis, it is generally the case that the agent ought to gamble, since the best possible outcome is to win the gamble, and that is possible only if you gamble. That is implausible on the face of it — and in that first example, we see that the gambler could make sure that gets 5 units by not gambling, which looks like a better option than the gamble, which may end with a gain of 10 or nothing at all. While someone who values gambling for its own risk might agree, we can’t think that this is what he ought to do. The second example is the same except that winning the gamble would only bring 5 units, with a risk of getting 0, while not gambling brings 5 for sure. In this case we think that he definitely ought not to gamble, but on the above analysis it is not true either that he ought to gamble or ought not to gamble.

Horty’s conclusion, surely correct, is that what is needed is a value ordering of the choices rather than of the possible outcomes (though there may, perhaps should, be) a connection between the two.

Fine, but Horty defines that ordering as follows: choice K’ (weakly) dominates choice K if none of the possible histories in K are better than any of those in K’. (See NOTES below, about this.) The analysis of ‘ought’ is then that the agent ought to see to it that A exactly if all his optimal choices make A definitely true.

Suppose the choice is between two lotteries, each of which sells a million tickets, and has a first prize of a million dollars, and a second prize of a thousand dollars. But only the second lottery has many consolation prizes worth a hundred dollars each. Of course there are also many outcomes of getting no prize at all. There is no domination to tell us which gamble to choose, but in fact, it seems clear that the choice should be the second gamble. That is because the expectation value of the second gamble is the greater.

This brings in the agent’s opinion, his subjective probability, to calculate the expectation value. It leads in this case to the right solution. And it does so too in the two examples above that Horty gave, if we think that the individual outcomes were in each case equally likely. For then in the first example the expectation value is 5 in either case, so there is no forthcoming ought. In the second example, the expectation value of gambling is 2.5, smaller than that of not gambling which is 5, so the agent ought not to gamble.

So, tentatively, here is my conclusion. Horty is right on three counts. The first is that the Chisholm/Meinong analysis, with its role for the value ordering of the possible outcomes, is faulty. The second is that the improvement needed is that we rely, in the analysis of ought statements, on a value ordering of the agent’s choices. And the third is that an integration with epistemic logic is needed, ….

…. but — I submit — with a logic of opinion rather than of knowledge.

NOTES

John Horty “Epistemic Oughts in Stit Semantics”. Ergo 6 (2019): 71-120

Horty’s definition of dominance is this:

K ≤ K’ (K’ weakly dominates K) if and only if Value(h) ≤ Value(h’) for each h in K and h’ in K’; and K < K’ (K’ strongly dominates K) if and only if K ≤ K’ and it is not the case that K’ ≤ K.

This ordering gives the right result for Horty’s second example (Ought not to gamble), while in the first example neither choice dominates the other. But the demand that all possible outcomes of choice K’ should be better than any in K seems to me too strong for a feasible notion of dominance. For example if the values of outcomes in one choice are 100 and 4, while in the other they are 5 and 4, this definition does not imply that the first choice weakly dominates the other, since 5 (in the second) is larger than 4 (in the first) — while intuitively, surely, the first choice should be advocated.

A temporal framework, plus

December 24, 2020January 4, 2021 Bas van FraassenLeave a comment

Motivation: I have been reading John Horty’s (2019) paper integrating deontic and epistemic logic with a framework of branching time. As a preliminary to exploring his examples and problem cases I want to outline one way to understand indeterminism and time, and a simple way in which such a framework can be given ‘attachments’ to accommodate modalities. Like Horty, I follow the main ideas introduced by Thomason (1970), and developed by Belnap et al. (2001).

The terms ‘branching time’ and ‘indeterminist time’ are not apt: it is the world, not time, that is indeterministic, and the branching tree diagram depicts possible histories of the world. I call a proposition historical if its truth or falsity in a world depends solely on the history of that world. At present I will focus solely on historical propositions, and so worlds will not be separately represented in the framework I will display here.

We distinguish what will actually happen from what it is settled now about what will happen. To cite Aristotle’s example: on a certain day it is unsettled, whether or not there will be a sea-battle tomorrow. However, what is settled does not rule out that there will be a sea-battle, and this too can be expressed in the language: some things may or can happen and others cannot.

Point of view: The world is indeterministic, in this view, with the past entirely settled (at any given moment) but the future largely unsettled. Whatever constraints there are on how things may come to be must derive from what has been the case so far, and similarly for whatever basis there is for our knowledge and opinion about the future. Therefore (?), our possible futures are the future histories of worlds whose history agrees with ours up to and through now.

Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true:

there will actually be a sea battle tomorrow, but it is possible that there will not be a sea battle tomorrow?

It can be true if ‘possible’ means ‘not yet settled that not’. (See Appendix for connection with Medieval puzzles about God’s fore-knowledge.)

Representation: A temporal framework is a triple T = <H, R, W>, where H is a non=empty set (the state-space), R is a set of real numbers (the calendar), W is a set of functions that map R into H (the trajectories, or histories). Elements of H are called the states, elements of R the times.

(Note: this framework can be amended, for example by restrictions on what R must be like, or having the set of attributes restricted to a privileged set of subsets of H, forming a lattice or algebra of sets, and so forth.)

Here is a typical picture to help the imagination. Note, though, that it may give the wrong impression. In an indeterministic world, possible futures may intersect or overlap.

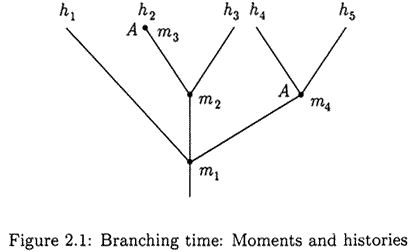If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.

An attribute is a subset of H, a proposition is a subset of W. For tense logic, what is more interesting is tensed propositions, which is to say, proposition-valued functions of time.

Basic propositions: if R is a region in the state-space H, the proposition R^(t) = {h in W: h(t) is in R} is true in history h at time t exactly if h(t) is in R. It is natural to read R^(t) as “it is R now”. If R is the attribute of being rainy then R^(t) would thus be read as “It is raining”.

I will let ‘A(t)’ stand for any proposition-valued function of time; the above example in which R is a region in H, is a special case. For any particular value of t, of course, A(t) is just a proposition, it is the function A(…) that is the tensed proposition. The family of basic propositions can be extended in many ways; first of all by allowing the Boolean set operations: A.B(t) = A(t) ∩ B(t), and so forth. We will look at more ways as we go.

Definitions:

worlds h and k agree through t (briefly h =/t k) exactly if h(t’) = k(t’) for all t’ ≤ t.
H(h, t)= {k in W: h =/ t k} is the t-cone of h, or the future cone of h at t, or the future cone of moment <h, t>.
SA(t)= {h in W: H(h, t) ⊆ A(t)}, the proposition that it is settled at t that A(t)

The term “future cone” is not quite apt since H(h, t) includes the entire past of h, which is common to all members of H(h, t). But the cone-like part of the diagram is the set of possible futures at for h at t.

Thus S, “it is settled that”, is an operator on tensed propositions. For example, if R is a region in the state-space then SR^(t) is true in h at t exactly if R has in it all histories in the t-cone of h. Logically, S is a sort of tensed S5-necessity operator. In Aristotle’s sea-battle example, nothing is settled on a certain evening, but early the next morning, as the fleets approach each other, it is settled that there will be a sea-battle.

There are two important notions related to settled-ness: a tensed proposition A(t) is backward-looking iff membership in A(t) depends solely on the world’s history up to and including t. That is equivalent to: A(t) is part of SA(t), and hence that A(t) = SA(t). If A is a region in H then A^(t) is backward-looking iff each future cone is either entirely inside A, or else entirely disjoint from A.

Similarly, A is sedate if h being in A(t) guarantees that h is in A(t’) for all t’ later than t (that world has, so to say, settled down into being such that A is true). Note well that a backward- looking proposition may be “about the future”, because in some respects the future may be determined by the past. Examples of sentences expressing such propositions:

“it has rained” is both backward-looking and sedate, “it will have rained” is sedate but not backward looking, and “it will rain” is neither.

Tense-modal operators can be introduced in the familiar way: “it will be A”, “it was A”, and so forth express obvious tensed propositions, e.g. FA(t) = {h in W: H(h,t’) ⊆ A for some t’> t}. More precise reckoning can also be introduced. For example if the numbers in the calendar represent days, then “it will be A tomorrow” expresses the tensed proposition TomA(t) = {h in W: h(t+1) is in A}.

Attachments

If T is a temporal framework then an attachment to T is any function that assigns new elements to any entities definable as belonging to T. The examples will make this clear.

Normal modal logic

Let T = <H, R, W> be a temporal framework and REL a function that assigns to W a binary relation on W. Define:

◊A^(t) = {h in W: for some k in W such that REL(h, k), k(t) is in A}

Read as the familiar ‘relative possibility’ relation in standard possible world semantics, a sentence expressing ◊A^(t) would be of the form “it is possible that it is raining”.

But such a modal logic has various instances. In addition to alethic modal logic, there is for example a basic epistemic logic where the models take this form. There, possibility is compatibility with the agent’s knowledge, ‘possible for all I know’. In that case a reading of ◊A^(t) would be “It is possible for all I know that it is raining”, or “I do not know that it is not raining”.

While deontic logic began as a normal modal logic, it has now a number of forms. An important development occurred when Horty introduced the idea of reasons and imperatives as default rules in non-monotonic logic. There is still, however, a basic form that is common, which we can here attach to a temporal framework.

To each moment we attach a situation in which an agent is facing choices. What ought to be the case, or to be done, depends on what it is best for this agent to do. Horty has examples to show that this is not determined simply by an ordering of the possible outcomes, it has to be based on what is best among the choices. (The better-than ordering of the choices can be defined from a better-than ordering of the possible outcomes, as Horty does. But that is not the only option; it could be based for example on expectation values.)

Let T = <H, R, W> be a temporal framework and SIT a function that assigns to each moment m = <h, t> a situation, represented by a family Δ of disjoint subsets of the future cone of m, plus an ordering of the members of Δ. The cells of Δ are called choices: if X is in Δ then X represents the choice to see to it that the actual future will be in X. The included ordering ≤ of sets of histories may be constrained or generated in various ways, or made to depend on specific factors such as h or t. Call X in Δ optimal iff for all Y in Δ, if X ≤ Y then Y ≤ X. Then one way to explicate ‘Ought’ is this:

OA(t) = {h in W: for some optimal member X of Δ in SIT(<h, t>), X ⊆ A(t)}

This particular formulation allows for ‘moral dilemmas’, that is cases in which more than one cell of Δ is optimal and each induces an undefeated obligation. That is, there may be mutually disjoint tensed propositions A(t) and B(t) such that a given history h is both in OA(t) and in OB(t), presenting a moral dilemma.

An alternative formulation could base what ought to be only on the choice that is uniquely the best, and insure that there is always such a choice that is ‘best, all considered’.

Subjective probability

We imagine again an agent in a situation at each moment <h, t>, this time with opinion, represented by a probability function P<h,t> defined on the propositions. (If the state-space is ‘big’ the attributes must be restricted to a Boolean algebra (field) of subsets of the state-space, and thus similarly restrict the family of propositions.)

This induces an assignment of probabilities to tensed propositions: thus if R is a region in H, P(R^(t)) = r is true in h at t exactly if P<h, t>({h in W: h(t) is in R}) = r. Similarly, the probability FR^(t) is true in h at t, is P<h,t>({{h in W: h(t’) is in R for some t’> t}). So if R stands for the rainy region of possible states, this is the agent’s opinion, in moment <h,t>, that it will rain.

In view of the above remarks about the dependency of future on the past, the subjective probabilities will tend to be severely constrained. One natural constraint is that if h =/t h’ then P<h,t> = P<h’,t>.

In Horty’s (2019) examples (which I would like to discuss in a sequel) it is clear that the agent knows (or is certain about) which futures are possible. In that case, at each moment, the future cone of that moment has probability 1. For any proposition A(t), its probability at <h, t> equals the probability of A(t) ∩ H(h, t).

APPENDIX

I am not unsympathetic to the view that only what is settled is true. But the contrary is also reasonable, and simpler to represent. However, we face the puzzle that I noted above, about whether it makes sense to say that we have different possible futures, though one is actual, and future tense statements are true or false depending on what the actual future is.

In the Middle Ages this came up as the question of compatibility between God’s foreknowledge and free will. If God, being omniscient, knew already at Creation that Eve would eat the apple, and that Judas would betray Jesus, then it was already true then that they would do that. Doesn’t that imply that it wasn’t up to them, that they had no choice, that nothing they could think of will would alter the fact that they were going to do that?

No, it does not imply that. God knew that they would freely decide on what they would do, and also knew what they would do. If that is not clearly consistent to you — as I suppose it shouldn’t be! — I would prefer to refer you to the literature, e.g. Zagzebski 2017.

REFERENCES

(I adapted the diagrams from this website)

Belnap, Nuel; Michael Perloff, and Ming Xu (2001) Facing the Future; Agents and Choices in our Indeterministic World. New York: Oxford University Press.

Horty, John (2019) “Epistemic Oughts in Stit Semantics”. Ergo 6: 71-120.

Müller T. (2014) “Introduction: The Many Branches of Belnap’s Logic”. In: Müller T. (eds) Nuel Belnap on Indeterminism and Free Action. Outstanding Contributions to Logic, vol 2. Springer, Cham. https://doi.org/10.1007/978-3-319-01754-9_1

Thomason, R. H. (1970) “Indeterminist Time and Truth Value Gaps,” Theoria 36: 264-281.

Zagzebski, Linda (2017) “Foreknowledge and Free Will“, The Stanford Encyclopedia of Philosophy (Summer 2017 Edition), Edward N. Zalta (ed.).