Blog Feed

Probabilities of Conditionals (1): finite set-ups

Bas van FraassenLeave a comment

If a theory has no finite models, can we still discuss finite examples, taking for granted that they can be represented in the theory’s models?

It is a well-known story:  Robert Stalnaker introduced the thesis, now generally called 

The Equation             P(p → q) = P(q|p), provided P(p) > 0

that the probability of a conditional is the conditional probability of consequent-given-antecedent.  Then David Lewis refuted Stalnaker’s theory.

In 1976 proposed The Equation for a weaker logic of conditionals that I called CE.  The main theorem was that any probability function P on a denumerable or finite field of sets (‘propositions‘) can be extended to a model of CE incorporating P, with an operation → on the propositions, satisfying The Equation.

To be clear:  the models for CE endowed with probability in this way are very large, the universe of possible worlds non-denumerable.  But taking a cue from the proof of that theorem,  I mean to show here that we can in practice direct our attention to finite set-ups.  These are, as it were, the beginnings of models, and they can be used to provide legitimate examples with manageable calculations.

The reason the theory’s models get so large is that the conditional probabilities introduce more and more numbers (See Hajek 1989).  

Example. Consider the possible outcomes of a fair die toss: 1, 2, 3, 4, 5, 6.  With these outcomes as possible worlds, we have 2^6 propositions, but all the probabilities assigned to them are multiples of 1/6.  So what is the conditional probability of the outcome is 5, given that it is not 6?  Probability 1/5.  What is the conditional probability of the outcome is 4, given the outcome is less than 5? Probability 1/4.  Neither is a multiple of 1/6.  

Therefore, none of those 2^6 propositions can be either the proposition that the outcome is (5 if it is not 6), or the proposition that the outcome is (4 if it is less than 5).

In the end, the only way to allow for arbitrarily nested conditionals, in any and all proposition algebras closed under →, is to think of any set of outcomes that we want to model as the slices of an equitably sliced pie which is infinitely divisible.  

The telling examples that we deal with in practice do not involve much nesting of conditionals.  So let us look into the tossed fair die example, and see how much we have to construct to accommodate simple examples.  I will call such a construction a set-up.

(In the Appendix I will give set-ups a precise definition of set-ups as partial models, but for now, will explain them informally.)

GENERAL: MODELS AND PROPOSITION ALGEBRAS

As do Stalnaker and Lewis, I define the → operation by using a selection function s: this function s takes any proposition p and any world x into a subset of p,  s(p, x).  

world y is in (p –> q) if and only if s(p, y) ⊆ q

The main constraint is that s(p, x) has at most one member.  It can be empty or be a unit set.  Secondly, if y is in p, then s(p, y) = {y}, and if p is empty then s(p, y) is empty too.  There are no other constraints.  

Specifically, unlike for Stalnaker and Lewis, the selection is not constrained by a nearness relation.  I do not take the nearness metaphor seriously, and see no convincing reason for such a constraint.  But I use the terminology sometimes, just as a mnemonic device to describe the relevant selection:  if s(p, x) = {y} I may call y the nearest p-world to x.  

The result of the consequent freedom is that if p and q are distinct propositions then the functions s(p, .) and s(q, .) are totally independent — each can be constructed independently, without any regard to the others.

That allows us to build parts of models while leaving out much that normally belongs in a model.

EXAMPLE: THE OUTCOMES OF A TOSSED DIE

A die is tossed, that has six possible outcomes, there are six possible worlds:  (1) is the world in which the outcome is 1, and similarly for (2), …, (6).  I will call this set of worlds S (mnemonic for “six”).   There is a probability function P on the powerset of S: it assigns 1/6 to each world.  I will refer to the set-up that we are constructing here as Set-Up 1.

As examples I will take two propositions:

p = {(1), (3), (5)}, “the outcome is odd”. This proposition is true just in worlds (1), (3), (5).

q = {(1), (2), (3)}, “the outcome is low”.  This proposition is true just in worlds (1), (2), (3) 

Each of these two propositions has probability 1/2.

The idea is now to  construct s(p,.) so that P(p → q) = P(q|p).  I claim no intuitive basis for the result. Its purpose is to show how the Equation can be satisfied while observing basic logic of conditionals CE.

It is clear that (p → q) consists of two parts, namely (p ∩ q) and a certain part of ~p.  Can we always choose a part of ~p so that the probabilities of these two parts add up to P(q|p)?  A little theorem says yes: 

               P(q|p) minus P(p ∩ q)  ≤   P(~p).

Of course at this point we can only do so where the only probabilities in play are multiples of 1/6.  Later we can look at others, and build a larger partial model.  I will show how the small set-up here will emerge then as part of the larger set-up, so nothing is lost.

For a given non-empty proposition p, we need only construct (p → {x}) for each x in p, making sure that their probabilities add up to 1.  The probabilities of the conditionals (p → r), for any other proposition r, are then determined in this set-up.  That is so because S is finite and in any proposition algebra (model of CE),

(p → t) ∪ (p → u) = [p → (t ∪ u)]

So let us start with member (1) of proposition p, and define s(p, .) so that P(p → {(1)}) = 1/3, which is the conditional probability P({(1)} | p).

That means that (p → {(1)}) must have two worlds in it, (1) itself and a world in ~p.  Therefore set

 s(p, (2)) = {(1)}.

Then (p→{(1)}) = {(1), (2)} which does indeed have probability 1/3.

Similarly for the others (see the diagram below, which shows it all graphically):

 s(p, (4)) ={ (3)},     s(p, (6)) = {(5)}

You can see at once how we will deal with s(~p,.)

s(~p, (1)) = {(2)},    s(~p, (3)) = {(4)},    s(~p, (5)) = {(6)}

so that, for example, (~p → {(2)}) = {(2), (1)}, which has probability 1/3, equal to the conditional probability P({(2)} | ~p).

What about (p –> {(6)})?  There is no world x such that s(p, x) = {6}.  So (p → {(6)}) is the empty set and P(p –> {(6)}) = 0, which is indeed P({(6)}|p).

Let’s see how this works for p with the other proposition q, “the outcome is low”; that is, the proposition q = {(1), (2), (3)}

 (p → q), “if the outcome is odd then it is low”, is 

  • true in (1) and (3) since they are in (p ∩  q), they are their own nearest p-worlds.
  • true in (2) and (4), since their nearest p-world are (1) and (3) respectively 
  • false in (5) and (6) since their nearest p-world is (5) “odd but not low”

(~p → q), “if the outcome is even, then it is low”, is

  • true in (2) since it is in ~p ∩ q
  • true in (1) since its nearest ~p-world is (2), “even and low”
  • false in (3), for its nearest ~p world is (4), “even and high”
  • false in (4), for it is its own nearest ~p world, “even and high”
  • false in (5), for its nearest ~p world is (6), “even and high”
  • false in (6), for it is its own nearest ~p world, “even and high”

So (p → q) is {(1), (3), (2), 4)} which has probability 2/3; ……….we verify that it is P(q|p)

     (~p → q) is {(2), (1)}, which has probability 1/3; ……………………..we verify that it is P(q|~p) 

A DIAGRAM OF THE MODEL: selection for antecedents p  and ~p

The blue arrows are for the ‘nearest p-world’ selection, and the red arrows for the ‘nearest ~p-world’ selection.

THE SECOND STAGE:  EXPANDING THE SET-UP

Above I gave two examples of conditional probabilities that are not multiples of 1/6, but of 1/4 and of 1/5.  In Set-Up 1 there is no conditional proposition that can be read as “if the outcome is not six then it is five”.  The arrow is only partially defined.  So how shall we improve on this?

Since the smallest number that is a multiple of all of 6, 4, and 5 is 60, we will need a set-up with 60 worlds in it, with 10 of them being worlds in which the die toss outcome is 1, and so forth.

So we replace (1) by the couples <1, 1>, <1, 2>, …., <1, 10>.  Similarly for the others.  I will write [(x)] for the set {<x, 1>, …, <x, 10>} Giving the Roman numeral X as name to {1, …, 10}, our set of worlds will no longer be S, but the Cartesian product SxX.  I will refer to the set-up we are constructing here as Set-Up 2. The probability function P is extended accordingly, and assigns the same probability 1/60 to each member of SxX.

Now we can construct the selection function s(u, .) for proposition u which was true in S in worlds (1), …, (5) – read it as “the outcome is not six” – and is true in our new set-up in the fifty worlds <1,1>, …, <5, 10>.  As before, to fix all the relevant probabilities, we need:

(u → [(t)]) has probability 1/5 for each (t), from 1 to 5.

Since [(t)] is the intersection of itself with u, it is part of (u → [(t)]).  That gives us ten elements of SxX, but since 1/5 = 12/60, we need two more.  They have to be chosen from ~u, that is, from [(6)]

Do it systematically:  divide ~u into five sets and let the selection function choose their ‘nearest’ in u appropriately:

s(u, <6, 1>) = {<1,1>}. <s(u, <6,2>) = {<1,2>}

s(u, <6, 3>) = {<2,1>}. <s(u, <6,4>) = {<2,2>}

s(u, <6, 5>) = {<3,1>}. <s(u, <6,6>) = {<3,2>}

s(u, <6, 7>) = {<4,1>}. <s(u, <6,8>) = {<4,2>}

s(u, <6, 9>) = {<5,1>}. <s(u, <6,10>) = {<5,2>}

So now (u → [(5)]) = {<5, 1>, …, <5, 10>, <6,9>, <6,10>}, which has twelve members, each with probability 1/60, and so this conditional has probability 1/5, which is the right conditional probability.

It will be clear enough now, how we can similarly construct s(r, .) for proposition r read as “the outcome is less than 5”, which requires conditional probabilities equal to ¼.

HOW SET-UP 1 RE-APPEARS IN SET-UP 2

And it should also be clear how what we did with propositions p and q in the earlier set-up, with universe of worlds S emerges in this larger set-up in the appropriate way.  For example, the proposition read as “the outcome is low” is now the union of [(1)], [(2)], and [(3)], and so forth.

Of course, there are new propositions now.  For some of these we can construct a selection function as well. For example, the proposition (u → [(5)]) which we just looked at has twelve members, and the probability 1/12 equals 5/60, a multiple of 1/60.  So we can construct the selection function s(u → [(5)]), .).  Thus for any proposition t, the proposition [(u → [(5)]) → t]  will be well-defined and its probability will be the relevant conditional probability.  But there are other propositions in Set-Up 2 for which this can be done only by embedding this set-up in a still larger one.

As I said above, eventually we have to look upon the six possible outcomes of the die toss as slices of an evenly divided pie, this pie being infinitely divisible.  That is a comment about the theorem proved for models of the logic CE in which The Equation is satisfied. But as long as our examples, the ones that play a role in philosophical discussions of The Equation, are “small” enough, they will fit into small enough set-ups.

APPENDIX.

While leaving more details to the 1976 paper, I will here distinguish the set-ups, which are partial models, from the models.

I will now use “p”, “q” etc. with no connection to their use for specific propositions in the text above.

A frame is a triple <V, F, P>, with V a non-empty set, F a field (Boolean algebra) of subsets of V, P a probability function on a field G of subsets of V, with F part of G.

A model is a quintuple <V, F, P, s, →> such that:

  •  <V, F, P> is a frame 
  • s (the selection function) is a function from FxV into the power set of V such that
  • s(p, x) has at most one member
  • if x is in p then s(p, x) = {x}
  • s(Λ, x) = Λ

→ is the binary function defined on FxF by the equation

(p → q)  = {x in V: s(p,x) ⊆ q}

Note: with this definition, <V, F, →>  is a proposition algebra, that is, a Boolean algebra with (full or partial) binary operation →, with the following properties (where defined):

(I)        (p → q) ∩ (p → r) =  [p → (q ∩ r)]

(II)       (p → q) ∪ (p → r) = [p → (q ∪ r)]

(III)     p ∩ (p →q)  =   p ∩ q

(IV)     (p → p) = V.

A set-up or partial model  is a quintuple <V, F, P, s, →> defined exactly as for a model, except that s is a partial function, defined only on a subset of FxV.  And accordingly, → is then a partial binary function on the propositions.

In the next post I will explore Set-Up 1 and Set-Up 2 further, with examples . 

NOTES 

I want to thank Branden Fitelson and Kurt Norlin for stimulating correspondence, which gave me the impulse to try to figure this out.  

REFERENCES

The theorem referred to above is on page 289 of my “Probabilities of Conditionals”, pp. 261-300 in W. Harper and C.A.Hooker (eds.), Foundations of Probability Theory, ….   Vol. 1. Reidel Pub; Dordrecht 1976.

(Note that this is not the part about Stalnaker-Bernoulli models, it is instead about the models defined on that page. There is no limit on the nesting of arrows.)

Alan Hajek, “Probabilities of Conditionals: Revisited”.  Journal of Philosophical Logic 18 (1989): 423-428.  (Theorem that the Equation has no finite models.)

Alan Hajek and Ned Hall, “The hypothesis of the conditional construal of conditional probability”.  pp. 75-111 in Probability and Conditionals: Belief Revision and Rational Decision.  Cambridge U Press 1994.

Deontic logic: arrows and imperatives

Bas van FraassenLeave a comment

A look at violations of three logical principles (Weakening, Transitivity, Import-Export) for analogies with imperatives, with a side-long glance at counterfactual conditionals and Chisholm’s paradox.

Arrows and imperatives are both binary functions on propositions.  We even use practically the same wording for both:

If the weather clears, we go on a picnic

If the weather clears, [do] go on a picnic!

So analogies may be illuminating– perhaps the difficulties we have often seen with arrows will point us to ideas about imperatives.

[1] Weakening

First, a good and very familiar reason for rejecting the material conditional as capturing conditionals in actual usage is the problem with the law of Weakening.  It has a precisely similar problem for imperatives:

[For conditionals] If it bursts into flame, we will go for the fire extinguisher.

Infer:

If it bursts into flame, and is immediately doused with water, we will go for the fire extinguisher.

[For imperatives] If it bursts into flame, [do] go for the fire extinguisher!

Infer:

If it bursts into flame, and is immediately doused with water, [do] go for the fire extinguisher!

In neither case is the inference correct.

[2] Transitivity

There is a similar problem with the law of Transitivity which holds both for material and strict conditionals.  Again, I see an analogy to imperatives:

If Hoover had been a Communist, he would have been a highly effective spy.

If Hoover been Russian, he would have been a Communist

Infer:

If Hoover been Russian, he would have been a highly effective spy.

We don’t accept the inference because we think that fanatical loyalty to his country was part of Hoover’s character.  But he might well have had sufficient epistemic distance to see what he would have to do in each case, so that for him the corresponding imperatives would be in force:

If you are a Communist, be a highly effective spy!

If you are Russian, be a Communist!

But he would not recognize or accept the imperative:

If you are Russian, be a highly effective spy!

Both the original example and the analogue for imperatives can be contested, in the way counterfactuals are in general. The objection is that the sort of language is context-dependent, and the two premises would not be true in the same context of discussion. The example loses all force if we spell out what was kept constant in each case:for the first premise, but not for the second, that Hoover was American.

Nevertheless, the logic of conditionals that was prompted by such examples, which involve counterfactuals, lacks Weakening and Transitivity.  So this may harbor suggestions for reasoning with imperatives. 

[3] Import-Export

The next familiar logical law to look at is Import-Export, which is the basic principle of Intuitionistic logic:

(A & B) –> C if and only if  A –> (B –>C)

This fails in counterfactual reasoning.  I’ll give the example that Branden Fitelson recently sent me.  A die is about to be cast, and we consider three propositions:

A: the outcome will be 1, 3, 5, or 6

B: the outcome will be even

C: the outcome will be 6

(A & B) is the same as C, so clearly  (A & B) –> C, no matter what.  The other side would be:

A –> (B –>C):  If the outcome were to be 1, 3, 5, or 6 then (if the outcome were to be even, then the outcome would be 6)

That may seem right at first blush, but it is refutable.  Take a model in which there are only two possible worlds, α and β.  Of course (A & B) –> C  is true in both.  Imagine we are in α,  where A is true but B and C are false, because the outcome is 1.  Then to evaluate the conditional in α,  we go to a possible situation β where B is true because the outcome is 2.  But then C is false in β. So we conclude that (B –> C) is false in α, where A is true.

What about imperatives, is there an analogy?  There are two ways to construe this question.

[ONE] Suppose that (A & B) implies C, and also that the imperative (Do A!) is in force.  Does it follow that then, by implication, (if B do C!) is in force? 

Counterexample:  take C to be just (A & B).  If (Do A!) is in force, does it follow, for any proposition B at all, that (If B, see to it that A & B!) is in force?  But that is equivalent to (if B, see to it that A!), regardless of what B is.  So no, definitely not!

[TWO] For the second way to think about this, let’s leave the example, which has the very special feature that C is equivalent to (A & B).  Let A, B, C be arbitrary factual propositions and suppose that (If A and B, see to it that C!) is in force.  Suppose A is true.  Does it follow that the imperative (If B, see to it that C!) is now in force? 

One question is whether a factual proposition can be such that, necessarily, if it is true then a certain imperative is in force.  This opens up a new subject, that requires much more comples modeling of decision situations than I have been thinking about so far. 

An example might be the factual proposition that the captain has ordered the soldier to stand guard.  As a result, the imperative (Stand guard!) is in force in the soldier’s situation.  And the soldier’s knowledge could include “If the captain has ordered me to stand guard then the imperative (Stand guard!) is in force for me.” 

But the Import-Export principle, if it is a logical law, then it must hold for any propositions, not just for such special ones that establish authority.  Suppose now that (If A and B, see to it that C!) is in force.  If the person knows that A is true, there are two possibilities: he also knows that B is true (in which case the imperative kicks in) or he does not know that B is true (so the imperative does not kick in).  What he knows then includes that:

if he were to come to know that B is true, he should see to it that C, if all the present imperatives are still in force

which reminds us of the previous discussion, about imperatives, time, and the Moebius strip.  We cannot assume in general that imperatives stay in force over time, that is a special case.  In our present reflection then, we have to say that even on this second way of taking the question, the answer is that the analogue to Import-Export fails.

[4] Chisholm’s Paradox

So far then we have, in view of those examples, come to the point where the arrow is interpreted as Stalnaker and Lewis do, allowing for counterfactual conditionals. With a side-long glance at a recent paper by Saint-Croix and Thomason (see NOTES below), let’s see how that fares in the old Chisholm’s paradox. I will add a time element, so that we can evaluate it in a situation before it is settled whether or not Jones goes to his neighbor’s help.

  1. It ought to be that Jones will go to help his neighbor tomorrow.
  2. It ought to be that if Jones will go to help his neighbor tomorrow then Jones tells his neighbor that he is going to come.
  3. If Jones does not go to help his neighbor tomorrow then Jones ought not to tell his neighbor that he is going to come.
  4. Jones does not go to help his neighbor tomorrow.

Suppose that we take the “if … then” in this example to be the conditional of Lewis or Stalnaker logic. Saint-Croix and Thomason point out the following. Let us start with a situation α in which Jones has promised to to help his neighbor tomorrow; as a result, 1. is true. It is not determined yet whether he will go to help his neighbor: that will happen tomorrow or not at all. Is premise 3. true?

To answer this, we look at the ‘nearest’ world to α, call it β, in which Jones does not go to help his neighbor the next day. Being ‘nearest’, it is true there too that Jones has promised to go help his neighbor. Is it true that he ought not to tell his neighbor that he is going to come? Not at all: in view of his promise, he ought to go to his neighbor’s aid the next day, and to tell him that he will do so.

Saint-Croix and Thomason respond to this by contextualizing the ‘nearest’ world selection, and their view as a whole is very attractive (though I am not yet ready to give up the rival view of conditional obligation statements as analogous to conditional probability statements). But however that may be, let us see how the Chisholm story plays out with imperatives.

Corresponding to the first three premises we imagine Jones in a situation α* where three imperatives are in force (using obvious abbreviations):

(Do Help!), (If Help, do Tell!), (If ~Help, do ~Tell!)

There are two scenarios for Jones’ action: (A) he both goes to help, and tells that he is going to come, (B) he does not go to help and does not tell that he is going to come. The former has the greater value, so in α* it is the case that he ought to go to help and tell that he will.

Now let us look at the next day, and suppose that he does not help his neighbor. Could all three imperatives still be in force.? The first has now become impossible to carry out, and there can be no obligation to do the impossible (as opposed to having two obligations which cannot both be satisfied). So no, the first imperative is no longer in force. The second may be, but does not kick in. The third, presumably still in force, does kick in and we conclude that on that next day, in which Jones does not go to his neighbor’s aid, he ought not to tell him that he is coming. Precisely the conclusion that common sense would suggest.

[5] Moral Conflicts

This discussion walks so closely to questions about conflict that it is timely to say that construing the “if … then” as a Stalnaker or Lewis arrow, in such examples, will not do at all if we are to accommodate genuine moral conflicts.

Look at the first two premises in Chisholm’s paradox. It is typical when this is discussed to say that together they imply that Jones ought to tell that he is going to come. Well, in Jones’ situation, if we imagine him as subject to the corresponding imperatives, he ought to do so, as we saw. But the pattern of inference cannot be generally valid for Ought statements, without eliminating the possibility of genuine moral conflicts:

5. Ought(A)

6. Ought(B)

7. B implies [if A then (A & B)] …. with “if then” as material implication

8. Ought[if A then (A & B)]

9. Ought(A & B)

Here 5 and 6 are premises, and 9 the unwelcome conclusion. The inference I meant was the one from 5 and 8 to 9:

Ought(X), Ought (if X then Y), therefore Ought(Y)

That is a standard inference form, in the present case connected with the similar

Z –> X, Z –> (if X then Y), therefore Z –> Y

and which thus needs to be rejected if we are to accommodate genuine moral conflicts.

As to the inference form 6 and 7 to 8, that is valid even in the minimal deontic logic that allows for conflicts, for it is a single-premise inference (recall Farjami’s “Up” ).

NOTES

Catharine Saint-Croix and Richmond H. Thomason “Chisholm’s Paradox and Conditional Oughts”. In Fabrizio Cariani et al., eds, Deontic Logic and Normative Systems:2014a, DEON 2014. Springer- Verlag, Berlin, 2014, pp. 192–207. Downloaded from https://web.eecs.umich.edu/~rthomaso/documents/deontic-logic/ctd.pdf

Deontic logic: the Moebius strip

Bas van FraassenLeave a comment

It happens rather often in a subject area that authors’ intuitions conflict with each other. It seems to me that Makinson’s ‘Moebius strip” problem (1999) may be the occasion of conflicting intuitions about what a person’s normative situation may or can be like. Or perhaps it is not different understandings of the same thing, but rather different projects in the same subject area. At the very least, the example looks different depending on whether or not we think about the situation developing in time.

I will present the Moebius Strip example below, but will first think through the way such a developing situation can be modeled.

[I] The Moebius Strip in STIT semantics

What I want to spell out for myself, first of all, is how the Moebius Strip might look in STIT semantics, that is, in a temporal development.

I will write “!E” for the imperative “See to it that E!”. Also, I will assume that seeing to it that something be the case, if it is not already the case, takes some time. Usually, perhaps, it takes only a moment, but sometimes (consider “!There is peace on earth”) a bit longer.

Let me begin with a situation S in which a certain set of imperatives are in force DELTA = {<!A(i), if B(i)>: i = 1, 2, …, n}, and what is known, in toto, is proposition K. I will here identify S as <K, DELTA, v>, where v summarizes other features that determine truth-values of statements in S. On this basis we should be able to determine which statements of form Ought(E) are true in that situation, in ways to be spelled out.

Just to make clear what it means to be in force, in contrast to how imperatives demand action, take this example. Tim is a soldier; the captain has ordered him to stand guard, and to sound the alarm if the enemy approaches. Both these imperatives are in force, and the first ‘kicks in’ (demands action) immediately, since it has no condition. The second condition ‘kicks in’ only if (or when) Tim knows that the enemy approaches.

The main points of interpretation

I propose to understand this situation (but realize that others may understand this differently), as follows:

(1) Seeing to it that E, if E is not true already, changes the person’s situation, it puts him in a situation T different from S, in which E is true. What T is like may depend on other factors, for example, aging of the persons involved.

(2) If a person sees to it that E, then in the situation thus produced, that person knows that E. In other words, the knowledge in the new situation is a proposition that implies E.

(3) O(E) is true in that situation exactly if the person in that situation ought to see to it that E is true.

(4) Ought(E) is true in S exactly if there is a subset J of {1, .., n} such that K implies all of {A(k): k in J}, the intersection of K with all of {A(k) ∩ B(k): k in J} is not empty, and the set J is maximal in this respect.

(5) The set of imperatives that are in force, in any given situation, cannot include one that is impossible to satisfy, in and by itself, given what is known in that situation. So for example in S, if K implies A(1) then the intersection of K, A(1), and B(1) is not empty. This is the point of the principle that ought implies can.

(6) In view of (1), (2), and (5) we cannot expect that all the imperatives in force in S will also all still be in force in the succeeding situation T, in general. The dynamics of the process that occurs when agents react to imperatives must have at least some independent features that determine which imperatives are in force in the succeeding elements of that process.

The Moebius Strip example, for tenseless propositions

How does the Moebius Strip example look, if these points are all accepted? The example is of a situation S* in which three imperatives are in force:

<!A, if B>, <!C, if A>, <!~B, if C>

Although not so specified, I assume that A, B, C are mutually independent propositions.

To determine which Ought statements are true in this situation we must first ask what is known then. There are different possibilities.

[a] K = T, the tautology. In that case, assuming that A, B, C are not tautologies, there is nothing that ought to be seen to.

[b] K implies A but not B. In that case the person ought to see to it that C, and subsequently see to it that ~B. For it is only when he knows that C that the imperative <!~B, if C> kicks in. Again, no problem appears.

[c] K implies B, but not A or C. In that case Ought(A) is the case; that is all. But then, if the person obeys and sees to it that A, he lands in situation S*[B], where A is true and is part of the knowledge then.

Now we need to ask another question: are we dealing with tensed or tenseless propositions? If the counter is wet I can see to it that it is dry (a moment later). But if the counter is wet at time t, I cannot see to it that it is dry at time t. And secondly, are we dealing with an ideal agent, not subject to forgetfulness, or a less ideal one?

Let us (first) focus on the special case: the propositions are tenseless, and the agent’s knowledge does not diminish over time. Therefore in S*[B], both A and B are known to be true.

Sub-case: The same imperatives are in force in S*[B] as in S*. The first demands no action now, since A is true. But the second kicks in, and Ought(C) is the case in S[B]. If the person then sees to it that C, he lands by similar reasoning in a new situation S*[B, C] where A, B, C are all known.

In that case, if all the same imperatives are in force in S*[B, C], Ought(~B) is true there. But that contradicts point (5), since B is known to be true. Therefore the imperative <!~C, B> is not in force in situation S*[B,C].

It seems to me this is the only interesting sub-case. The suspected difficulty cannot arise, there is no possible situation sequence in which we land in a self-contradiction.

Is this counterintuitive? Do imperatives lose their force when it comes to be known that they cannot be satisfied? Imagine I have promised to give you a horse if you come home for Christmas. What happens to this promise if it turns out at Christmas that I have no horse to give you? I will have secondary obligations (I have to make this up to you), but (whatever I may have done wrong), it is not true at Christmas time that I ought to be giving you a horse. That promise has dropped out, the question of keeping it has become moot (though not without other moral consequences).

The Moebius Strip for tensed propositions

It may be objected here that I focused on too easy a case, by taking the propositions to be tenseless. Of course, if B is tenseless, and known to be true, then any imperative to see to it that ~B can’t even be in force, for it asks the impossible.

So what if we take the propositions to be tensed? Here is an example:

  • If there is a fire in the garage, get the fire extinguisher
  • If you have the the fire extinguisher, extinguish any fire in the garage
  • If there is no fire in the garage, bring the fire extinguisher back

In our official phrasing this involves the tensed propositions expressed as follows:

  • !See to it that you have the fire extinguisher, if there is a fire in the garage
  • !See to it that there is no fire in the garage, if you have the fire extinguisher
  • !See to it that you do not have the fire extinguisher, if there is no fire in the garage

This has the temporal sequence written on its face, so to speak, and no scenario presents any semblance of difficulty.

In one scenario, I already have the fire extinguisher, I make sure that there is no fire in the garage (by inspection or action), and then bring the fire extinguisher back to where it normally belongs. On another scenario, I learn and hence know that there is a fire in the garage. The first imperative kicks in, and I see to it that I have the fire extinguisher. At this point, again, I see to it that there is no fire in the garage, and when that is so, the third imperative kicks in and I return the fire extinguisher.

[II] Alternative Understanding of Situation: Makinson, Horty

So, what alternative understanding of a decision situation would lead one to adjust one’s logic, in response to the Moebius Strip example? Makinson answer this in section 3.2.4, with Example 4, intended to show that using a focus on maximally consistent subsets of the norms does not give the intuitively correct result.

Example 4 (Möbius strip). Let C = {(α,β), (γ,α), (~β,γ)}. Intuitively, we would like to have α, γ and not(β). But …

This intuition is geared to a non-temporal understanding of the imperatives: if it is known that β then the first and second imperatives are to be simultaneously obeyed. The reason is that the first is seen as bringing the second along with it.

This would certainly be the case if obeying it were to take no time at all (to be instantaneous), and to effect no change in the situation. It would also be appropriate if the imperatives are in a subject area where time is not a relevant concern — perhaps commands in a program designed to perform mathematical calculations?

That same intuition appears to be Horty’s in his book, when he introduces the notion that one imperative can trigger another, by making true, and known, the antecedent of the other. Again, that assumes that the situation is not changed in two steps but in one, and thus either ignores time as irrelevant (as it may indeed be in certain cases) or assumes the action to be instantaneous.

REFERENCES

Makinson, David “On a fundamental problem of deontic logic”, pp 29-53 in Norms, Logics and Information Systems. New Studies in Deontic Logic and Computer Science, edited by Paul McNamara and Henry Prakken (Amsterdam: IOS Press, Series: Frontiers in Artificial Intelligence and Applications, Volume: 49, 1999, ISBN 9051994273)

Horty, John F. Reasons as Defaults. Oxford: Oxford University Press, 2012.

Deontic logic: meta-imperatives?

Bas van FraassenLeave a comment

(This is a reflection on Jorg Hansen’s “Imperative logic and its problems”)

I am not sure whether there is reasoning from imperatives to imperatives, but there does seem to be reasoning from imperatives to ‘ought’ statements. Say, Tim is a soldier and his captain has ordered him to stand guard. Then Tim ought to stand guard. Or, I have promised to meet you for lunch. Then I ought to meet you for lunch. My promise has had the same effect as the captain’s order: in my situation I am now subject to an imperative (!Meet him for lunch!), which is in force (not defeated or in any other way deprived of force), so I ought to see to it that it is satisfied (that I meet you for lunch).

This reasoning from a premise that a certain imperative is in force to a conclusion stating that something ought to be (or be done) appears to be central to the subject of deontic logic, the subject of normative reasoning. It seems so basic that it must perhaps be accepted as logically necessary, or as necessary by virtue of the meanings of the terms involved. I don’t mean to dispute that (though I have no idea what sort of necessity it is). But I do see some complexities and some questions I feel I need to face.

As preliminary, let’s take an old example. Suppose two imperatives are in force: !Honor your parents! and !Do not honor your father! Does valid reasoning from the existence of these two imperatives lead to the conclusion that I ought to honor my mother?

Perhaps so, but in that case it must be non-monotonic reasoning. For if there were an additional imperative in force, !Do not honor your mother!, I would be in a situation of moral conflict, and it is not clear what I ought to do. Prima facie, yes, I ought to honor my mother, and also my father, and also not honor them … But all things considered? There may be no answer, or there may be an answer that draws on additional features of my situation, not mentioned so far.

Let’s go back to soldier Tim and his captain. The example seemed straightforward because we naturally read it as describing a situation in which there was only one imperative in force. Actually, there were also many standing orders, and perhaps an order by the lieutenant, and promises Tim had made, and so forth. Should the principle if you are subject to an (undefeated) imperative to do X you ought to do X be extrapolated to if you are subject to many (undefeated) imperatives you ought to satisfy them all ? The move from each to all seems inescapable here, though we know that in other contexts it may be invalid.

In the case of a moral conflict, you can’t satisfy them all. It may still be true for each of those imperatives that you ought to comply, but it cannot be true that you must comply with all, since that is impossible.

So if we cannot reason from each to all in this case, how should we reason? I know what I want to say, I just don’t know whether it is something I can justify. What I want to say is:

[IMP] if you are subject to many (undefeated) imperatives, satisfy a maximally consistent set of those imperatives!

(In the case of a moral conflict, merely satisfying this does not necessarily lead to a unique thing you ought to do. I realize that, but it seems to me step one.)

But what is the status of [IMP]? Is it an imperative to which we are all subject? What gives it force (if it is in fact in force)? Is it a meta-imperative, or perhaps we should say, a higher-order imperative that governs reasoning from imperatives? if so, what could bring a meta-imperative into force? I’m going to have to think about this.

Is [IMP] defeasible?

Is [IMP], just as any other imperative, defeasible? An authority might explicitly issue a permission:

[PERM] if you cannot do all that, just do any or none, just as you like!

Actually, I don’t think that this is an instance of defeasibility, for [PERM] is not a higher-order imperative. For suppose that [PERM] is added to a set [S] of imperatives. Then this addition will not subtract from the family of maximally consistent sets of imperatives in force, though it will add some. And the calculation of what ought to be need not be seen as any different: for [PERM] is (or can be expressed as) an ordinary imperative, not a meta- or higher-order imperative.

Example: Imperatives 1, 2, 3 are to do A, B, C, which are not jointly satisfiable, but any two of which are compatible. Hence there are three maximally consistent sets. Now add imperative 4: !if you have any difficulty, just do one or none! If the agent does not know of any difficulty, nothing changes in what she ought to do, for the addition is a conditional imperative. But if such knowledge is added, then there are four possibilities for action, of which three are maximally consistent (satisfying 4 alone by not doing any of 1, 2, 3, is not maximal).

So, unless there are theoretical considerations (whether for or against, or for ways of qualifying it) that have not occurred to me, I would say that [IMP] is at least not a defeasible imperative.

Two points in favor of [IMP]

Meanwhile I note that [IMP] settles the examples about honoring your parents in the right way. If !Honor your parents! and !Do not honor your father! are the only imperatives in force, they form a maximally consistent set (the only one) and so you should satisfy both, which you can only do by honoring your mother (only). If however !Honor your parents! and !Do not honor your father! and !Do not honor your mother! are all in force then there are three maximally consistent subsets, and the only thing you ought not to do is to honor both your father and your mother. Which, as Bertrand Russell would have said, is just the conclusion that would have been reached by common sense.

Another way to check our intuitions is to imagine how someone might be called to account, and what would count as a good defense. So imagine that I live in a communal house, and through some unforeseen circumstances I end up, 40 minutes beforehand, facing three household chores to complete before dinner. Each would take 20 minutes: washing the lunch dishes, cleaning the dining room, managing the dishes that are already cooking. Impossible! At dinner I am called to account.

Scenario 1. “I did none of the three. My excuse is that it was impossible for me to do all that I ought to have done.”

This is fairly clearly unacceptable.

Scenario 2. “I did one of the three: I cleaned the dining room. My excuse is that it was impossible for me to do all that I ought to have done.”

The obvious retort is that I had time to do two of the tasks, and ought to have done so.

Scenario 3. “I did two of the three: I washed the dishes and cleaned the dining room. My excuse is that it was impossible for me to do all that I ought to have done.”

There may be resistance to this, on the basis that the third task, managing the cooking, was the most important. But the retort will not be that I did fewer or less of what I ought to have done. Except that we have a pointer here to the need for a value ranking of the admissible alternative, this tale of an accounting supports the intuitive appeal of [IMP]. We ought to do the most of what we ought to do, if we cannot do all that we ought to do.

Anecdotes and intuitive appeal are all very well — I still wonder if there are theoretical ways to support meta-imperatives, or higher-order imperatives, whatever we should call them, like [IMP]?

REFERENCES

Jorg Hansen “Imperative logic and its problems”. Pp. 137-191 in D. Gabbay et al. Eds. Handbook of Deontic Logic and Normative Systems. College Publications 2013.

Deontic logic: value-rankings

Bas van FraassenLeave a comment

The historical opening chapter of the Handbook of Deontic Logic and Normative Systems shows that, in various forms, this has been a typical way to connect ‘ought’ statements with values:

[O] It ought to be that A if and only if it is better that A than that ~A

as well as

[Cond O] It ought to be that A, on supposition that B if and only if it is better that (B & A) than that (B & ~A)

But in addition, deontic logics typically include the law that carries logical implication into the derivation of ‘ought’ statements:

[IMP] If A implies B then (It ought to be that A) implies (It ought to be that B)

(and the similar law for conditional ‘ought’ statements), important to keep the logic within the range of normal modal logics.

But do [O] and [IMP] go well together? That depends on the character of the value ranking which defines the ‘better than’ relation among propositions. Specifically, it requires that

[MON] If A implies B, and A is better than ~A, then B is better than ~B.

Problem: I will give examples below of ‘better than’ relations which do have property MON but which are intuitively unsatisfactory. But a ranking by expectation value does not have property MON.

Ranking by expectation value does not have MON: For example, a bank robber is confronted by the police. His best option (by expectation value) is to surrender. What about the option to (surrender or resist arrest)? This is America! If he resists arrest he will likely be shot. That lowers the expectation value considerably. (Reminiscent of Ross’ paradox, also about IMP.)

Solution: There is something right about [O] and [CondO], namely that value rankings have an important role to play in the understanding of ‘ought’ statements. But there is also something wrong about [O] and [CondO], namely that they presuppose that it is just, and only, value rankings that must determine the status of ‘ought’ statements.

But let me first give examples of rankings that do have MON and say why I find them unsatisfactory. In my own essay on deontic logic as a normal modal logic (1972) I gave this definition:

Ought(A) is true exactly if opting for ~A precludes the attainment of some value which it is possible to attain if one opts for A

or less informally,

Ought(A) is true in possible world h exactly if, there are worlds satisfying A which have a higher value than any worlds that satisfy ~A.

Very unsatisfactory! Today I opted not to buy a lottery ticket, thereby precluding a million dollar windfall (larger than anything I could get otherwise) and so I was wrong. I ought to have bought that ticket! As gamblers say, when you talk about prudence, “Yes, but what if you win!” Sorry, gamblers — this is not a good guide to life …

Jeff Horty offered a more sophisticated formulation in his 2019 paper (p. 78, the Evaluation Rule) as his explication of the Meinong/Chisholm analysis, which would in a normal modal logic context amount to:

Ought(A) is true in world h exactly if A is true in all worlds h’ possible relative to h, such that there is no world h” which satisfies ~A and has a value higher than h’.

Except for the relativization of possibility, this is like the preceding. Horty rightly rejects this as unsatisfactory, using the example of a forced choice between two gambles which has the same expectation value, but of which one carries no risk of loss. (One has outcomes 10 and 0, the other has only outcome 5 with certainty.) It is certainly not warranted to say that we ought always to make the gamble with the higher prize but higher risk.

There are surely other value rankings to to try, and I thought of this one:

Ought(A) is true in world h exactly if there is a one-to-one function f mapping the worlds that satisfy ~A into the worlds that satisfy A, such that for all worlds h in the domain of f the value h is less than the value of f(h).

This one too has property MON. Informally put, it means that whatever outcome you get if you opt for ~A, you realize you might have done better by choosing for A.

But imagine: gamble ~ A has with certainty one of the outcomes 5, 7, or 9 dollars, while gamble A has with certainty one of the outcomes 1, 10, 12, 14 dollars. However, to make gamble A you have to buy a ticket for $4. So your net outcomes for A are loss of $3, or win of 6, 8, 10. Clearly by the above principle you should take gamble A, for 5 < 6 < 7 <8 < 9 < 10. But is that really the right thing to do? If all the outcomes are equally likely then ~A has expectation value (21/3) and A has expectation value (21/4), which is less.

In previous posts I have discussed how Horty goes beyond this.

Now I just want to explain how the use of expectation value ranking works well with what I proposed some weeks ago in the post Deontic logic: two paradoxes” (which I gave a more precise formulation in the next post, “Deontic logic: Horty’s new examples”.) By “works well” I mean that the principle [IMP] is valid.

My proposal was that in setting up the framework for deontic logic, , we need to include both imperatives and values. So I envisage the agent as first of all recognizing the imperatives in force in his situation (‘if you have sinned, repent!’). The agent’s next step is to take account of the satisfaction regions for those imperatives (or better, maximally consistent sets of them). Then the value-ranking is applied to those satisfaction regions, and the ones that count are the ones that get highest value (the optimal regions). Next:

It ought to be that A if and only if there is an optimal region that implies A.

(This can be extended to conditional oughts in the way Horty does: go look at the alternative situation in which the agent has the condition added to his knowledge.)

When entered at this point, it does not matter whether the ranking has property MON. For what ever the ranking is, if an optimal region is part of A, and A is part of B, then an optimal region is part of B.

The story for choices, decisions and action planning is similar. It is not that the agent ought to do what is best, but rather that he has to make a best choice (the moral of Horty 2019). Suppose it is already settled that I will gamble, and I have a choice between several gambles. Now what ought to be the case (about what I do, about my future) is whatever is implied by my making a best choice. And I propose that the best choices are those which are represented by propositions (the choices themselves, not the possible outcomes of those choices) which have highest expectation value.

Deontic logic: Horty’s gambles (2)

Bas van FraassenLeave a comment

In the second part of his 2019 paper Horty argues that there is a need to integrate epistemic logic with deontic logic, for “ought” statements often have a sense in which their truth-value depends in part on the agent’s state of knowledge.

I agree entirely with his conclusion. But is the focus on knowledge not too strict? Subjectively it is hard to distinguish knowledge from certainty — and apart from that, when we don’t have certainty, we are still subject to the same norms. So I would like to suggest that rational opinion, in the form of the agent’s actual subjective probability, is what matters.

Here I will examine Horty’s additional examples of gambling situations with that in mind. I realize that this is not sufficient to demonstrate my contention, but it will show clearly how the intuitive examples look different through the eyes of this less traditional epistemology.

Horty’s figure 4 depicts the following situation: I pay 5 units to be offered one of two gambles X1, X2 on a coin toss. My options will be to bett Heads, to bet Tails, or Not To Gamble. But I will not know which gamble it is! You, the bookmaker will independently flip a coin to determine that, and not tell me the outcome. In the diagram shown here, X1 is the gamble on the left and X2 the gamble on the right.

On Horty’s initial analysis, if in actual fact I am offered X1 then I should bet Heads, since that has the best outcome. But as he says, rightly, I could not be faulted for not doing that, since I did not know whether I was being offered X1 or X2.

Even if the conclusion is the same, the situation looks different if the agent acts on the basis of the expectation values of the options available to him. The alternatives depicted in the diagram are equi-probable (we assume the coins are fair). So for the agent, who has paid 5 units, his net expectation value for betting Heads (in this situation where it is equally probable that he is betting in X1 or in X2) is the average of gaining 5 and losing 5. The expectation value is 0. Similarly for the option of betting Tails, and similarly for the option of Not Gambling: each has net expectation value 0. So in this situation it just is not true that the agent ought to take up any of these options — it is indifferent what he does.

Horty offers a second example, where the correct judgment is that I ought not to gamble, to show that his initial analysis failed to entail that. Here is the diagram, to be interpreted in the same way as above — the difference is in the value of the separate possible outcomes.

Reasoning by expectation value, the agent concludes that indeed she ought not to gamble. For by not gambling the payoff is 5 with certainty, while the expectation value of Betting Heads, or of Betting Tails, is 2.5.

So on this analysis as well we reach the right conclusion: the agent ought not to gamble.

Entirely in agreement with Horty is the conclusion that these situations are adequately represented only if we bring epistemology into play. What the agent ought to do is not to be equated with what it would objectively, in a God’s eye, be best for her to do. It is rather what she ought to do, given her cognitive/epistemic/doxastic situation in the world. But she cannot make rational gambling decisions in general if her knowledge (or certainty) is all she is allowed to take into account.

It would be instructive to think also about the case in which it is known that the coin has a bias, say that on each toss (inlcuding the hidden first toss) it will be three times as likely as not to land heads up. Knowledge will not be different, but betting behavior should.

Deontic logic: Horty’s gambles (1)

Bas van FraassenLeave a comment

In “Epistemic oughts in Stit Semantics” Horty’s main argument is that an epistemic logic must be integrated in a satisfactory deontic logic. This is needed in order to account for a sense of what an agent ought to do hinges on a role for knowledge (“epistemic oughts”).

That argument occupies the second part of his paper, and I hope to explore it in a later post. But the first part of the paper, which focuses on a general concept of what an agent ought to do (ought to see to) is interesting in itself, and crucial for what follows. I will limit myself here to that part.

I agree with a main conclusion reached there, which is that the required value ordering is not of the possible outcomes of action but of the choices open to the agent.

However, I have a problem with the specific ordering of choices that Horty defines, which it seems to me faces intuitive counterexamples. I will propose an alternative ordering principle.

At a given instant t an agent has a variety V(h, t) of possible futures in history h. I call V(h, t) the future cone of h at t. But certain choices {K, K’, …} are open to the agent there, and by means of a given choice K the agent may see to it that the possible futures will be constrained to be in a certain subset V(K, h, t) of V(h, t).

The different choices are represented by these subsets of V(h, t), which form a partition. Hence the following is well defined for histories in V(m): the choice made in history h at t is the set V(K, h, t) to which h belongs; call it CA(h, t), thinking of “CA” as standing for “actual choice”.

In the diagram K1 is the set of possible histories h1 and h2, and so CA(h1,t) = K1 = CA(h2, t). (Note well: I speak in terms of instants t of time, rather than Horty’s moments.

And the statement that the agent sees to it that A is true in in h at t exactly if A is true in all the possible futures of h at t that belong to the choice made in history h at t. Briefly put: CA(h, t) ⊆ A.

The Chisholm/Meinong analysis of what ought to be is precisely what it is maximally good to be the case. Thus, at a given time, it ought to be that A if A is the case in all the possible future whose value is maximal among them. So applied to a statement about action, that means: It ought to be that the agent sees to it that A is true in h at t exactly if all the histories in the choice made in history h at t are of maximal value. That is, if h is in CA(h, t) and h’ is in V(h, t) but outside CA(h, t) then h’ is no more valuable than h.

But this analysis is not correct, as Horty shows with two examples of gambles. In each case the target proposition is G: the agent gambles, identified with the set of possible histories in which the agent takes the offered gamble. This is identified with: the agent sees to it that G. Hence the two choices, K1 and K2, open to the agent in h at t are represented by the intersection of V(h, t) with G and with ~G respectively.

In the first example the point made is that according to the above analysis, it is generally the case that the agent ought to gamble, since the best possible outcome is to win the gamble, and that is possible only if you gamble. That is implausible on the face of it — and in that first example, we see that the gambler could make sure that gets 5 units by not gambling, which looks like a better option than the gamble, which may end with a gain of 10 or nothing at all. While someone who values gambling for its own risk might agree, we can’t think that this is what he ought to do. The second example is the same except that winning the gamble would only bring 5 units, with a risk of getting 0, while not gambling brings 5 for sure. In this case we think that he definitely ought not to gamble, but on the above analysis it is not true either that he ought to gamble or ought not to gamble.

Horty’s conclusion, surely correct, is that what is needed is a value ordering of the choices rather than of the possible outcomes (though there may, perhaps should, be) a connection between the two.

Fine, but Horty defines that ordering as follows: choice K’ (weakly) dominates choice K if none of the possible histories in K are better than any of those in K’. (See NOTES below, about this.) The analysis of ‘ought’ is then that the agent ought to see to it that A exactly if all his optimal choices make A definitely true.

Suppose the choice is between two lotteries, each of which sells a million tickets, and has a first prize of a million dollars, and a second prize of a thousand dollars. But only the second lottery has many consolation prizes worth a hundred dollars each. Of course there are also many outcomes of getting no prize at all. There is no domination to tell us which gamble to choose, but in fact, it seems clear that the choice should be the second gamble. That is because the expectation value of the second gamble is the greater.

This brings in the agent’s opinion, his subjective probability, to calculate the expectation value. It leads in this case to the right solution. And it does so too in the two examples above that Horty gave, if we think that the individual outcomes were in each case equally likely. For then in the first example the expectation value is 5 in either case, so there is no forthcoming ought. In the second example, the expectation value of gambling is 2.5, smaller than that of not gambling which is 5, so the agent ought not to gamble.

So, tentatively, here is my conclusion. Horty is right on three counts. The first is that the Chisholm/Meinong analysis, with its role for the value ordering of the possible outcomes, is faulty. The second is that the improvement needed is that we rely, in the analysis of ought statements, on a value ordering of the agent’s choices. And the third is that an integration with epistemic logic is needed, ….

…. but — I submit — with a logic of opinion rather than of knowledge.

NOTES

John Horty “Epistemic Oughts in Stit Semantics”. Ergo 6 (2019): 71-120

Horty’s definition of dominance is this:

K ≤ K’ (K’ weakly dominates K) if and only if Value(h) ≤ Value(h’) for each h in K and h’ in K’; and K < K’ (K’ strongly dominates K) if and only if K ≤ K’ and it is not the case that K’ ≤ K.

This ordering gives the right result for Horty’s second example (Ought not to gamble), while in the first example neither choice dominates the other. But the demand that all possible outcomes of choice K’ should be better than any in K seems to me too strong for a feasible notion of dominance. For example if the values of outcomes in one choice are 100 and 4, while in the other they are 5 and 4, this definition does not imply that the first choice weakly dominates the other, since 5 (in the second) is larger than 4 (in the first) — while intuitively, surely, the first choice should be advocated.

Puzzling over indeterminism and tense

Bas van FraassenLeave a comment

(this follows on the post ‘Temporal framework’)

At this moment our history branches into many possible futures: that is how we depict the rejection of determinism.

But that rejects only forward determinism: the future is not uniquely determined by the past. When the typical, usual diagram of branching futures is drawn, we see no intersections or overlaps of futures. So it retains backward determinism: each momentary state has a unique past.

The puzzle I have is this: apparent violations of backward determinism are much easier to imagine, or even experience, than violations of forward determinism.

Example: Here I have in my hand a marble, and before me a metal bowl. I am freely choosing where to release the marble along the margin of the bowl: the marble has as many possible future trajectories as I have choices. Now I release it, and after some to and fro, it rests at the bottom: an equilibrium state is reached. Given this state, there is no possible retrodiction of its path, no way to determine where it was released. Every trajectory that begins with my releasing the marble at the margin ends up with the same final state: rest at the center of the bowl. So backward determinism is violated (unless there are hidden variables that have recorded its history). If we take into account only histories (of salient variables), we have to admit that they intersect or overlap, that from the equilibrium state they branch backward.

Talking about this (a long time ago) my friend Bob Meyer, an astute logician, said he was sure that time branched backward. “I go by inference to the best explanation”, he said, “nothing could so well account for how I ended up having so many more obligations than I every thought I had. I must have contracted many of them in alternative histories which now overlap in this moment.”

The problem I see, though, is that admitting this into a temporal framework would raise havoc with the analysis of tensed language. Suppose two histories h and h’ differ at noon today in that “It rained yesterday” is true in h and “It did not rain yesterday” is true in h’. Now add the supposition that h and h’ coincide in the interval (noon, noon+1). Immediately after noon, what truth-value has “It rained yesterday”?

When I look at how Horty presents the STIT semantics (or indeed many other discussions of branching time or tense logic which takes indeterminism seriously) I see it taken for granted that branching futures do not intersect.

That removes the puzzle by default or by fiat. I cannot fault that. It is the simplest thing to do. But it evades the problem, and leaves the puzzle intact.

There is a second solution: haecceity. That is, we can admit some factor that distinguishes histories even if the same trajectory is described in state space. The obvious candidate: the identity of the world whose history it is.

It is not too difficult to amend the scheme for a temporal framework to do that. A model structure now has a set K of worlds, a set T of numbers representing times, and for each world w a function h(w) mapping T into the state-space H. That function h(w) is the history of world w). A proposition must now be a set of worlds, but a typical proposition could still be

{w: h(w)(t) is in region R in the state space},

whose truth value in a world, at a time, depends solely on the history of that world.

More generally, a proposition is historical iff membership in it depends only on a world’s history. A proposition is metaphysical if it is not historical.

After the temporal framework is amended in this way, discussion can proceed as before, with the guarantee that even worlds which share all, or any part, of their history are distinct. The evaluation of tensed sentences at a time t may be different in worlds w and w’ even if h(w)(t) = h(w’)(t). The relevant diagrams show forward branching only.

In practice it may be best to just draw the upward branching diagrams and assume for simplicity that there are not, at any time, worlds with overlapping possible futures. Then the difference between worlds and histories can be ignored.

But just for conceptual clarity, I’ll spell out what the conscientiously amended framework would be.

APPENDIX. The Amended Temporal Framework

Representation: A temporal framework is a quadruple T = <K, H, R, W>, where K is a non-empty set (the worlds), H is a non=empty set (the state-space), R is a set of real numbers (the calendar), W is a set of functions that map K x R into H (the trajectories, or histories). Elements of H are called the states, elements of R the times. If h is a member of W and α world in K, then h(α) is the function h(α)(t) = h(α, t) which maps R into H. The function h(α) is the history of world α.

An attribute is a subset of H, a proposition is a subset of K. For tense logic, what is more interesting is tensed propositions, which is to say, proposition-valued functions of time.

Basic propositions: if R is a region in the state-space H, the proposition R^(t) = {α in K: h(α, t) is in R} is true in world α at time t exactly if h(α) is in A(t). It is natural to read A(t) as “it is A now”. If A is the attribute of being rainy then A(t) would thus be read as “It is raining”.

A moment is a triple <h, α, t> such that h(α, t) is the state of h at t.

  • worlds α and β agree through t (briefly α =/t β) exactly if h(α)(t’) = h(β)(t’) for all t’ ≤ t.
  • H(h, α, t)= {β in K: α =/ t β} is the t-cone of α, or the future cone of α at t, or the future cone of moment <h, α, t>.
  • SA(t)= {α in K: H(h, α, t) ⊆ A(t)}, the proposition that it is settled at t that A(t)

A proposition A is historical if and only if h(α) = h(β) implies that α is in A iff β is in A. A proposition is metaphysical iff it is not historical.

This distinction will mainly come into play if attachments introduce non-historical notions. For example, a modality might be introduced to accord with the metaphysical notion of a law of nature: β is possible relative to α if and only if the laws of nature in α are also laws of nature in β. Two worlds could have different laws of nature, but due to initial or boundary conditions still have the same history. In that case, if we define

◊A(t) = {α in K: for some β in K such that β is possible relative to α, h(β)(t) is in A}

then ◊A(t) will be a metaphysical tensed proposition.

A temporal framework, plus

Bas van FraassenLeave a comment

Motivation: I have been reading John Horty’s (2019) paper integrating deontic and epistemic logic with a framework of branching time. As a preliminary to exploring his examples and problem cases I want to outline one way to understand indeterminism and time, and a simple way in which such a framework can be given ‘attachments’ to accommodate modalities. Like Horty, I follow the main ideas introduced by Thomason (1970), and developed by Belnap et al. (2001).

The terms ‘branching time’ and ‘indeterminist time’ are not apt: it is the world, not time, that is indeterministic, and the branching tree diagram depicts possible histories of the world. I call a proposition historical if its truth or falsity in a world depends solely on the history of that world. At present I will focus solely on historical propositions, and so worlds will not be separately represented in the framework I will display here.

We distinguish what will actually happen from what it is settled now about what will happen. To cite Aristotle’s example: on a certain day it is unsettled, whether or not there will be a sea-battle tomorrow. However, what is settled does not rule out that there will be a sea-battle, and this too can be expressed in the language: some things may or can happen and others cannot.

Point of view: The world is indeterministic, in this view, with the past entirely settled (at any given moment) but the future largely unsettled. Whatever constraints there are on how things may come to be must derive from what has been the case so far, and similarly for whatever basis there is for our knowledge and opinion about the future. Therefore (?), our possible futures are the future histories of worlds whose history agrees with ours up to and through now.

Among the possible futures we have one that is actual, it is what will actually happen. This has been a subject of controversy; how could the following be true:

there will actually be a sea battle tomorrow, but it is possible that there will not be a sea battle tomorrow?

It can be true if ‘possible’ means ‘not yet settled that not’. (See Appendix for connection with Medieval puzzles about God’s fore-knowledge.)

Representation: A temporal framework is a triple T = <H, R, W>, where H is a non=empty set (the state-space), R is a set of real numbers (the calendar), W is a set of functions that map R into H (the trajectories, or histories). Elements of H are called the states, elements of R the times.

(Note: this framework can be amended, for example by restrictions on what R must be like, or having the set of attributes restricted to a privileged set of subsets of H, forming a lattice or algebra of sets, and so forth.)

Here is a typical picture to help the imagination. Note, though, that it may give the wrong impression. In an indeterministic world, possible futures may intersect or overlap.

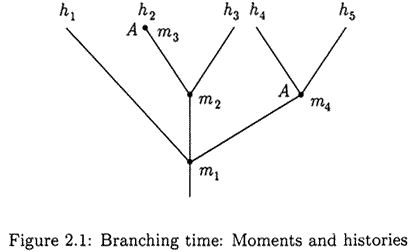If h is in W and t in R then h(t) is the state of h at time t. Since many histories may intersect at time t, it is convenient to use an auxiliary notion: a moment is a pair <h, t> such that h(t) is the state of h at t.

An attribute is a subset of H, a proposition is a subset of W. For tense logic, what is more interesting is tensed propositions, which is to say, proposition-valued functions of time.

Basic propositions: if R is a region in the state-space H, the proposition R^(t) = {h in W: h(t) is in R} is true in history h at time t exactly if h(t) is in R. It is natural to read R^(t) as “it is R now”. If R is the attribute of being rainy then R^(t) would thus be read as “It is raining”.

I will let ‘A(t)’ stand for any proposition-valued function of time; the above example in which R is a region in H, is a special case. For any particular value of t, of course, A(t) is just a proposition, it is the function A(…) that is the tensed proposition. The family of basic propositions can be extended in many ways; first of all by allowing the Boolean set operations: A.B(t) = A(t) ∩ B(t), and so forth. We will look at more ways as we go.

Definitions:

  • worlds h and k agree through t (briefly h =/t k) exactly if h(t’) = k(t’) for all t’ ≤ t.
  • H(h, t)= {k in W: h =/ t k} is the t-cone of h, or the future cone of h at t, or the future cone of moment <h, t>.
  • SA(t)= {h in W: H(h, t) ⊆ A(t)}, the proposition that it is settled at t that A(t)

The term “future cone” is not quite apt since H(h, t) includes the entire past of h, which is common to all members of H(h, t). But the cone-like part of the diagram is the set of possible futures at for h at t.

Thus S, “it is settled that”, is an operator on tensed propositions. For example, if R is a region in the state-space then SR^(t) is true in h at t exactly if R has in it all histories in the t-cone of h. Logically, S is a sort of tensed S5-necessity operator. In Aristotle’s sea-battle example, nothing is settled on a certain evening, but early the next morning, as the fleets approach each other, it is settled that there will be a sea-battle.

There are two important notions related to settled-ness: a tensed proposition A(t) is backward-looking iff membership in A(t) depends solely on the world’s history up to and including t. That is equivalent to: A(t) is part of SA(t), and hence that A(t) = SA(t). If A is a region in H then A^(t) is backward-looking iff each future cone is either entirely inside A, or else entirely disjoint from A.

Similarly, A is sedate if h being in A(t) guarantees that h is in A(t’) for all t’ later than t (that world has, so to say, settled down into being such that A is true). Note well that a backward- looking proposition may be “about the future”, because in some respects the future may be determined by the past. Examples of sentences expressing such propositions:

“it has rained” is both backward-looking and sedate, “it will have rained” is sedate but not backward looking, and “it will rain” is neither.

Tense-modal operators can be introduced in the familiar way: “it will be A”, “it was A”, and so forth express obvious tensed propositions, e.g. FA(t) = {h in W: H(h,t’) ⊆ A for some t’> t}. More precise reckoning can also be introduced. For example if the numbers in the calendar represent days, then “it will be A tomorrow” expresses the tensed proposition TomA(t) = {h in W: h(t+1) is in A}.

Attachments

If T is a temporal framework then an attachment to T is any function that assigns new elements to any entities definable as belonging to T. The examples will make this clear.

Normal modal logic

Let T = <H, R, W> be a temporal framework and REL a function that assigns to W a binary relation on W. Define:

◊A^(t) = {h in W: for some k in W such that REL(h, k), k(t) is in A}

Read as the familiar ‘relative possibility’ relation in standard possible world semantics, a sentence expressing ◊A^(t) would be of the form “it is possible that it is raining”.

But such a modal logic has various instances. In addition to alethic modal logic, there is for example a basic epistemic logic where the models take this form. There, possibility is compatibility with the agent’s knowledge, ‘possible for all I know’. In that case a reading of ◊A^(t) would be “It is possible for all I know that it is raining”, or “I do not know that it is not raining”.

Deontic logic

While deontic logic began as a normal modal logic, it has now a number of forms. An important development occurred when Horty introduced the idea of reasons and imperatives as default rules in non-monotonic logic. There is still, however, a basic form that is common, which we can here attach to a temporal framework.

To each moment we attach a situation in which an agent is facing choices. What ought to be the case, or to be done, depends on what it is best for this agent to do. Horty has examples to show that this is not determined simply by an ordering of the possible outcomes, it has to be based on what is best among the choices. (The better-than ordering of the choices can be defined from a better-than ordering of the possible outcomes, as Horty does. But that is not the only option; it could be based for example on expectation values.)

Let T = <H, R, W> be a temporal framework and SIT a function that assigns to each moment m = <h, t> a situation, represented by a family Δ of disjoint subsets of the future cone of m, plus an ordering of the members of Δ. The cells of Δ are called choices: if X is in Δ then X represents the choice to see to it that the actual future will be in X. The included ordering ≤ of sets of histories may be constrained or generated in various ways, or made to depend on specific factors such as h or t. Call X in Δ optimal iff for all Y in Δ, if X ≤ Y then Y ≤ X. Then one way to explicate ‘Ought’ is this:

OA(t) = {h in W: for some optimal member X of Δ in SIT(<h, t>), X ⊆ A(t)}

This particular formulation allows for ‘moral dilemmas’, that is cases in which more than one cell of Δ is optimal and each induces an undefeated obligation. That is, there may be mutually disjoint tensed propositions A(t) and B(t) such that a given history h is both in OA(t) and in OB(t), presenting a moral dilemma.

An alternative formulation could base what ought to be only on the choice that is uniquely the best, and insure that there is always such a choice that is ‘best, all considered’.

Subjective probability

We imagine again an agent in a situation at each moment <h, t>, this time with opinion, represented by a probability function P<h,t> defined on the propositions. (If the state-space is ‘big’ the attributes must be restricted to a Boolean algebra (field) of subsets of the state-space, and thus similarly restrict the family of propositions.)

This induces an assignment of probabilities to tensed propositions: thus if R is a region in H, P(R^(t)) = r is true in h at t exactly if P<h, t>({h in W: h(t) is in R}) = r. Similarly, the probability FR^(t) is true in h at t, is P<h,t>({{h in W: h(t’) is in R for some t’> t}). So if R stands for the rainy region of possible states, this is the agent’s opinion, in moment <h,t>, that it will rain.

In view of the above remarks about the dependency of future on the past, the subjective probabilities will tend to be severely constrained. One natural constraint is that if h =/t h’ then P<h,t> = P<h’,t>.

In Horty’s (2019) examples (which I would like to discuss in a sequel) it is clear that the agent knows (or is certain about) which futures are possible. In that case, at each moment, the future cone of that moment has probability 1. For any proposition A(t), its probability at <h, t> equals the probability of A(t) ∩ H(h, t).

APPENDIX

I am not unsympathetic to the view that only what is settled is true. But the contrary is also reasonable, and simpler to represent. However, we face the puzzle that I noted above, about whether it makes sense to say that we have different possible futures, though one is actual, and future tense statements are true or false depending on what the actual future is.

In the Middle Ages this came up as the question of compatibility between God’s foreknowledge and free will. If God, being omniscient, knew already at Creation that Eve would eat the apple, and that Judas would betray Jesus, then it was already true then that they would do that. Doesn’t that imply that it wasn’t up to them, that they had no choice, that nothing they could think of will would alter the fact that they were going to do that?

No, it does not imply that. God knew that they would freely decide on what they would do, and also knew what they would do. If that is not clearly consistent to you — as I suppose it shouldn’t be! — I would prefer to refer you to the literature, e.g. Zagzebski 2017.

REFERENCES

(I adapted the diagrams from this website)

Belnap, Nuel; Michael Perloff, and Ming Xu (2001) Facing the Future; Agents and Choices in our Indeterministic World. New York: Oxford University Press.

Horty, John (2019) “Epistemic Oughts in Stit Semantics”. Ergo 6: 71-120.

Müller T. (2014) “Introduction: The Many Branches of Belnap’s Logic”. In: Müller T. (eds) Nuel Belnap on Indeterminism and Free Action. Outstanding Contributions to Logic, vol 2. Springer, Cham. https://doi.org/10.1007/978-3-319-01754-9_1

Thomason, R. H. (1970) “Indeterminist Time and Truth Value Gaps,” Theoria 36: 264-281. 

Zagzebski, Linda (2017) “Foreknowledge and Free Will“, The Stanford Encyclopedia of Philosophy (Summer 2017 Edition), Edward N. Zalta (ed.).

Deontic logic: consequence relations

Bas van FraassenLeave a comment

Note:  this is a reflection on Ali Farjami’s Up operator — I would like to think about it in a very simple context, to begin.

That logic is mainly about consequence relations, and that these correspond to closure operators, was a theme introduced, I believe, by Tarski.  A closure operator C on sets of sentences has these characteristics:

(a) X ⊆ C(X)

(b) if Y ⊆ X then C(Y) ⊆ C(X)

 (c) C(C(X) ⊆ C(X)

From these it follows that C(C(X) =  C(X).

A set  X is called C-closed, or a C-theory, exactly if X = C(X).

The most familiar closure operator in logic is the one that corresponds to to the most familiar consequence relation:

            Cn(X) = {A:  X├A}

and a Cn-theory is just called a theory.

However there is another consequence relation, introduced in discussion of deontic logic, in effect, by Farjami.  Here the consequences of any and all single members of the set are gathered together, but there is not ‘putting together of premises’.  To indicate the reference to Farjami’s Up operator, I’ll call it Cu:

            Cu(X) = the union of the sets {A: B├A} for members B of X

or equivalently:

            Cu(X) = ∪{Cn(B): B a member of X}

That Cu has properties (a), (b), and (c)  is clear, so it is a closure operator.  We can call the relation of B to X if B is in Cu(X) a consequence relation for that reason, though it is very different from the usual one.

The difference from Cn is clearly that, for example, (A & B) is a member of Cn({A, B}) but not of Cu({A, B}). 

A Cu-theory is often not consistent, in the usual sense:  Cu({A, ~A}) does not contain any explicitly self-contradictions (in general, e.g. if A is atomic), but it is clearly not classically consistent.

But this is just why Cu can represent the proper consequences of a set of commands, imperatives, inputs, or instructions, when that set may harbor conflicts — and hence useful to deontic logics which countenance irresolvable moral conflicts.

There is an definition of consistency, however, that can apply non-trivially to a Cu-theory. Call it A-consistency: a Cu-theory is A-consistent iff it does not contain all sentences (equivalently, it does not contain any sentence that is a classical self-contradiction).

So let us see how that can work, let us focus on the following minimal deontic logic which I will call VHC:

A1. Axiom and rule schemata for classical sentential logic

A2. ├~O(~A &A)

R1. if ├A and ├A  ⊃ B, then ├ B

R2. if ├ A ⊃ B, then ├ O(A) ⊃ O(B)

There is a corresponding consequence relation, ‘ ├ in VHC‘ .

It is quite clear what those axioms and rules tell us:

a theory in VHC is a theory X in classical sentential logic with this characteristic, that the set {A: OA is in X} is an A-consistent Cu-theory.

A simple way to model this would be to think of a possible world model: in each world there is an agent who recognizes a certain set of sentences as expressing the primary obligations in force — thus, OA is true in this situation exactly if one of those primary obligation sentences implies A.

But this is too simple, it ignores infinity. A Cu-theory may not be ‘axiomatizable’, it may not be possible to sum it up in that way. Suppose a1, a2, a3, … are the countably many atomic sentences in the language, and let Y = {a1, (a1 & a2), (a1, & a2 & a3), ….}. Then there is no sentence B such that Cu(Y) = Cu(B). In fact there is no finite set Z of sentences such that Cu(Y) = Cu(Z).

We may call a set like Cu({a,b}) finitely generated, but if a, b are logically independent, such as two atomic sentences, then there is no sentence B such that Cu({a, b}) is the same as either Cu(B) or Cn(B). We are used to finite descriptions allowing for a ‘summing up’ in a single sentence, but that is not the case for Cu-theories.

Here we have the motivation to think in terms of the algebra of propositions instead of logic of sentences. In a possible world semantics the propositions are the sets of worlds, hence form a Boolean algebra which is complete. Even in infinitely descending chain of ever stronger propositions has an infimum which is a proposition (every maximal filter is a principal filter).

So the way to set up a possible world model structure is to associate with each world α a set I(α) of propositions. Then when the truth conditions of sentences are spelled out, so that each sentence A expresses a proposition |A|, the condition for “it ought to be” is:

OA is true in α if and only if there is a proposition Q in I(α) such that Q ⊆ |A|

or equivalently

|OA| = {α: there is a proposition Q in I(α) such that Q ⊆ |A|}

which shows clearly that the connective O corresponds to an operator on propositions.

Soundness and completeness for VHC can be discussed with this clue:

the set of sentences true in a world is a maximal theory in VHC, and that is a set of sentences X which is a theory in classical sentential logic, negation complete, and such that {A: OA is in X} is an A-consistent Cu-theory.

Now, how shall we think about those cases in which the Cu-theory in question is not ‘axiomatizable’? It is a situation in which there are more primary obligations than the agent could have spelled out for himself, even in principle, in the language s/he has.

It seems to me that this is the sort of world we live in. In Roman times even the Christians did not realize that slavery is wrong — that was a moral insight that we, Western people, did not yet have. Perhaps this is typical. Not only perhaps, it seems to me, but likely, and I would frame this as something that philosophers writing on ethics, who are not logicians, do not seem to have:

Infinity: for every moral norm in which we gain insight, there is yet another one.